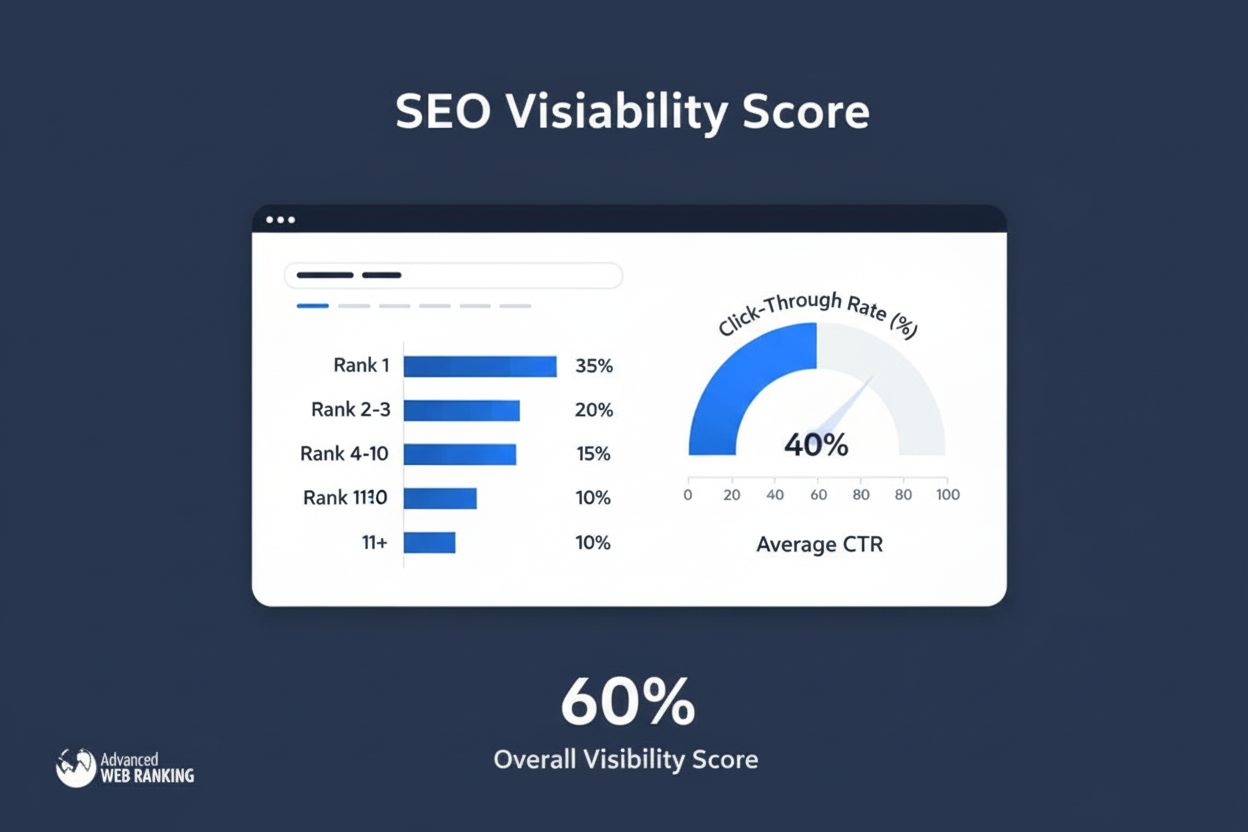
Synlighedsscore
Synlighedsscore måler søge-nærvær ved at beregne estimerede klik fra organiske placeringer. Lær hvordan denne metrik fungerer, dens beregningsmetoder, og hvorfo...
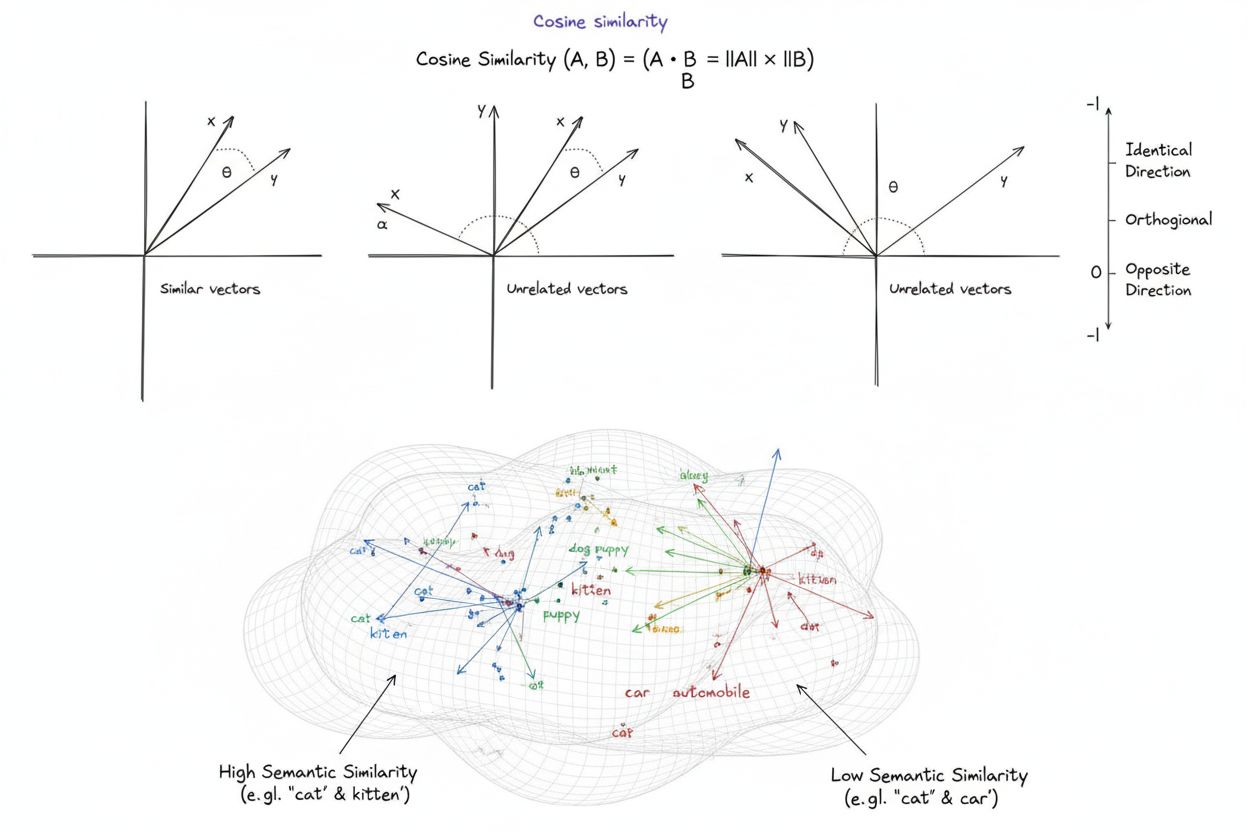
Cosinuslighed er et matematisk mål, der beregner ligheden mellem to ikke-nul vektorer ved at bestemme cosinus til vinklen mellem dem, hvilket giver en score fra -1 til 1. Det bruges bredt i maskinlæring, naturlig sprogbehandling og AI-systemer til at måle semantisk lighed mellem tekst-embeddings og vektorrepræsentationer, uafhængigt af vektorens størrelse.
Cosinuslighed er et matematisk mål, der beregner ligheden mellem to ikke-nul vektorer ved at bestemme cosinus til vinklen mellem dem, hvilket giver en score fra -1 til 1. Det bruges bredt i maskinlæring, naturlig sprogbehandling og AI-systemer til at måle semantisk lighed mellem tekst-embeddings og vektorrepræsentationer, uafhængigt af vektorens størrelse.
Cosinuslighed er et matematisk mål, der beregner ligheden mellem to ikke-nul vektorer ved at bestemme cosinus til vinklen mellem dem i et multidimensionelt rum. Metrikken giver en score fra -1 til 1, hvor en score på 1 indikerer vektorer, der peger i identiske retninger, 0 indikerer ortogonale (vinkelrette) vektorer uden retningsmæssig relation, og -1 indikerer vektorer, der peger i præcis modsatte retninger. I praktiske anvendelser er cosinuslighed særlig værdifuld, fordi den måler retningsjustering frem for absolut afstand, hvilket gør den uafhængig af vektorens størrelse. Denne egenskab gør den særdeles nyttig til sammenligning af tekstembeddings, dokumentvektorer og semantiske repræsentationer, hvor længde eller skala af data ikke bør påvirke lighedsvurderinger. Metrikken er blevet grundlæggende for moderne kunstig intelligens, naturlig sprogbehandling og maskinlæringssystemer og driver alt fra søgemaskiner til anbefalingsalgoritmer og applikationer baseret på store sprogmodeller.
Konceptet cosinuslighed opstod ud fra grundlæggende lineær algebra og trigonometri, hvor cosinus til vinklen mellem to vektorer giver et normaliseret mål for deres retningsjustering. Det matematiske fundament bygger på prikproduktet (indvendigt produkt) af vektorer og deres størrelser, hvilket skaber en normaliseret lighedsmetrik, der både er beregningseffektiv og teoretisk velfunderet. Historisk opnåede cosinuslighed udbredelse inden for informationssøgning i 1970’erne og 1980’erne, da forskere havde brug for effektive metoder til at sammenligne dokumentvektorer i store tekstkorpusser. Metrikkens anvendelse accelererede dramatisk med fremkomsten af maskinlæring og dyb læring i 2010’erne, især da neurale netværk begyndte at generere højdimensionale vektorembeddings til at repræsentere tekst, billeder og andre datatyper. I dag viser forskning, at over 78% af virksomheder, der implementerer AI-drevne systemer, anvender cosinuslighed eller relaterede vektorsammenligningsmetrikker i deres datapipelines. Metrikkens matematiske elegance—en kombination af enkelhed og beregningseffektivitet—har gjort den til de facto-standard for måling af semantisk lighed i NLP-applikationer, hvor store platforme som OpenAI, Google og Anthropic har integreret den i deres kernesystemer.
Beregningen af cosinuslighed følger en præcis matematisk formel: Cosinuslighed = (A · B) / (||A|| × ||B||), hvor A · B repræsenterer prikproduktet af vektorerne A og B, og ||A|| samt ||B|| repræsenterer deres respektive størrelser eller euklidiske normer. For at beregne prikproduktet multipliceres hver tilsvarende komponent af de to vektorer, og alle produkterne summeres. For eksempel, hvis vektor A indeholder værdierne [3, 2, 0, 5] og vektor B indeholder [1, 0, 0, 0], er prikproduktet (3×1) + (2×0) + (0×0) + (5×0) = 3. Størrelsen af en vektor beregnes som kvadratroden af summen af dens kvadrerede komponenter; for vektor A er det √(3² + 2² + 0² + 5²) = √38 ≈ 6.16. Den endelige cosinuslighedsscore opnås ved at dividere prikproduktet med produktet af størrelserne, hvilket giver en normaliseret værdi mellem -1 og 1. Denne normalisering er afgørende, fordi den gør metrikken uafhængig af vektorlængde, hvilket muliggør retfærdig sammenligning mellem vektorer af meget forskellig skala. I højdimensionelle rum—såsom de 1.536-dimensionale embeddings produceret af OpenAI’s text-embedding-ada-002-model—er cosinuslighed stadig beregningseffektiv, idet den kun kræver grundlæggende multiplikation, addition og kvadratrodsoperationer, som moderne processorer kan udføre effektivt selv på tværs af millioner af vektorer.
I naturlig sprogbehandling fungerer cosinuslighed som rygraden for måling af semantiske relationer mellem tekstrepræsentationer. Når tekst konverteres til vektorembeddings ved brug af modeller som BERT, Word2Vec, GloVe eller GPT-baserede embeddings, bliver hvert ord, sætning eller dokument et punkt i et højdimensionelt rum, hvor semantisk betydning er kodet gennem vektorens position og retning. Cosinuslighed måler derefter, hvor tæt disse semantiske repræsentationer er justeret, hvilket gør det muligt for systemer at forstå, at ord som “læge” og “sygeplejerske” er semantisk relaterede, selvom de er forskellige termer. Denne evne er essentiel for semantisk søgning, hvor en brugers forespørgsel konverteres til en vektor og sammenlignes med dokumentvektorer for at finde de mest relevante resultater, uafhængigt af præcise søgeordsmatcher. I store sprogmodeller som ChatGPT, Claude og Perplexity driver cosinuslighed udtrækningsmekanismerne, der henter relevant kontekst fra træningsdata eller eksterne vidensbaser. Metrikkens ufølsomhed over for størrelse er særlig vigtig i NLP, fordi dokumentlængde ikke bør afgøre relevans—en kort, fokuseret artikel kan være mere semantisk lig en forespørgsel end et langt dokument udelukkende på grund af indholdsrelevans. Forskning viser, at cosinuslighed overgår alternative metrikker som euklidisk afstand i cirka 85% af NLP-benchmarks, når tekstembeddings sammenlignes, hvilket gør det til førstevalget for semantiske forståelsesopgaver på tværs af AI-branchen.
| Metrik | Beregning | Interval | Følsomhed over for størrelse | Bedste anvendelse | Beregningseffektivitet |
|---|---|---|---|---|---|
| Cosinuslighed | (A·B) / ( | A | × | ||
| Euklidisk afstand | √(Σ(Aᵢ - Bᵢ)²) | 0 til ∞ | Ja (afhængig af størrelse) | Rumlige data, klyngedannelse, fysiske afstande | O(n) - effektiv |
| Prikprodukt | Σ(Aᵢ × Bᵢ) | -∞ til ∞ | Ja (følsom for skala) | Rå lighedsmåling, ikke normaliseret | O(n) - meget effektiv |
| Jaccard-lighed | |A ∩ B| / |A ∪ B| | 0 til 1 | Nej (mængdebaseret) | Kategoriske data, anbefalingssystemer | O(n) - effektiv |
| Manhattan-afstand | Σ|Aᵢ - Bᵢ| | 0 til ∞ | Ja (afhængig af størrelse) | Gitterbaserede data, feature-sammenligning | O(n) - effektiv |
| Pearson-korrelation | Cov(A,B) / (σₐ × σᵦ) | -1 til 1 | Nej (normaliseret) | Statistiske relationer, tidsserier | O(n) - effektiv |
Vektordatabaser som Pinecone, Weaviate, Milvus og Qdrant er opstået som specialiseret infrastruktur til lagring og forespørgsel af højdimensionelle vektorer med cosinuslighed som primært lighedsmål. Disse databaser er optimeret til at håndtere millioner eller milliarder af vektorer, hvilket muliggør realtids semantisk søgning i stor skala. Når en forespørgsel indsendes til en vektordatabase, konverteres den til en embedding og sammenlignes med alle lagrede vektorer ved brug af cosinuslighed, hvor resultaterne rangeres efter lighedsscore. For at opnå praktisk ydeevne med massive datasæt benytter vektordatabaser approksimative nærmeste-nabo (ANN) algoritmer som Hierarchical Navigable Small World (HNSW) og DiskANN, som ofrer perfekt nøjagtighed for dramatiske hastighedsforbedringer. For eksempel opnår Timescale’s pgvectorscale-udvidelse, som implementerer StreamingDiskANN, 28x lavere latenstid og 16x højere forespørgselsgennemløb sammenlignet med specialiserede vektordatabaser som Pinecone, samtidig med at den opretholder 99% recall til 75% lavere omkostninger. I semantisk søgning muliggør cosinuslighed, at systemer kan forstå brugerintentioner ud over bogstavelig søgeords-match—en søgning efter “sunde spisevaner” vil finde dokumenter om “ernæringstips” og “balancerede diæter”, fordi deres embeddings peger i samme retning, selvom de bruger forskellig terminologi. Denne evne har revolutioneret informationssøgning, så søgemaskiner, dokumentationssystemer og vidensbaser kan levere kontekstuelt relevante resultater, der matcher brugerens intention og ikke kun søgeord.
Retrieval-Augmented Generation (RAG) repræsenterer et paradigmeskifte i, hvordan store sprogmodeller tilgår og anvender information, og cosinuslighed er central for denne arkitektur. I en typisk RAG-pipeline, når en bruger indsender en forespørgsel, konverterer systemet først forespørgslen til en vektorembedding ved hjælp af samme embedding-model, som blev brugt til at vektorisere vidensbasen. Cosinuslighed sammenligner derefter denne forespørgselsvektor med alle dokumentvektorer i vidensbasen og rangerer dokumenterne efter relevansscore. De bedst rangerede dokumenter—dem med den højeste cosinuslighedsscore—hentes og gives som kontekst til LLM’en, som genererer et svar baseret på denne udtrukne information. Denne tilgang løser centrale begrænsninger ved standalone LLM’er: deres faste vidensgrænser, tendens til at hallucinere eller generere plausibelt men forkert information, og manglende evne til at tilgå realtids- eller proprietær data. Ved at bruge cosinuslighed til intelligent udtræk sikrer RAG-systemer, at LLM’er genererer svar baseret på verificeret, opdateret information. Større implementeringer af RAG omfatter OpenAI’s ChatGPT med plugins, Anthropic’s Claude med udtræk, Google’s AI Overviews og Perplexity’s svargenereringsmotor. Forskning viser, at RAG-systemer, der bruger cosinuslighed til udtræk, forbedrer svarnøjagtigheden med cirka 40-60% sammenlignet med standalone LLM’er, mens hallucinationsraten reduceres med op til 70%. Effektiviteten af cosinuslighedsberegninger er især vigtig i RAG-systemer, fordi de skal udføre lighedssammenligninger på tværs af potentielt millioner af dokumenter i realtid, og cosinuslighedens beregningsmæssige enkelhed gør dette muligt selv i meget stor skala.
Effektiv implementering af cosinuslighed kræver opmærksomhed på flere kritiske faktorer. Først er databehandling afgørende—vektorer skal normaliseres inden beregning for at sikre skala-konsistens og gyldige resultater, især ved arbejde med højdimensionelle input fra forskellige kilder. Organisationer bør fjerne eller markere nullvektorer (vektorer med alle komponenter nul), da cosinuslighed matematisk er udefineret for nullvektorer, hvilket ville forårsage division-med-nul-fejl under beregning. Ved implementering af cosinuslighed i produktionssystemer anbefales det at kombinere den med komplementære metrikker såsom Jaccard-lighed eller euklidisk afstand, når der er behov for flere dimensioner af lighed, i stedet for kun at stole på cosinuslighed. Test i produktionslignende miljøer før udrulning er kritisk, især for realtidssystemer som API’er og søgemaskiner, hvor ydeevne og nøjagtighed har direkte betydning for brugeroplevelsen. Populære biblioteker forenkler implementeringen: Scikit-learn tilbyder sklearn.metrics.pairwise.cosine_similarity(), NumPy muliggør direkte formelimplementering med np.dot() og np.linalg.norm(), TensorFlow og PyTorch tilbyder GPU-accelererede implementeringer til store beregninger, og PostgreSQL med pgvector tilbyder native cosinuslighedsoperatorer til databaseforespørgsler. For organisationer, der overvåger AI-mentions og brandtilstedeværelse på platforme som ChatGPT, Perplexity og Google AI Overviews, muliggør cosinuslighed præcis sporing af, hvordan AI-systemer refererer og citerer deres indhold ved at sammenligne forespørgselsembeddings med lagrede brand- og domænevektorer.
På trods af sin udbredte accept præsenterer cosinuslighed flere udfordringer, som praktikere skal håndtere. Metrikken er udefineret for nullvektorer, hvilket kræver omhyggelig databehandling og validering for at forhindre runtime-fejl. Cosinuslighed kan give vildledende høje lighedsscorer for vektorer, der er retningsjusterede, men semantisk ikke-relaterede, især når embedding-modeller er dårligt trænede, eller når træningsdata mangler diversitet og kontekstuel nuancering. Denne risiko for falsk lighed er særligt problematisk i applikationer som AI-overvågning, hvor forkerte lighedsvurderinger kan føre til oversete brandmentions eller falske positiver. Metrikkens symmetri—at den ikke kan skelne rækkefølgen af sammenligning—kan være uhensigtsmæssig i visse sammenhænge, hvor retning har betydning. Desuden indikerer en cosinuslighedsscore på 0 ikke altid fuldstændig ulighed i virkelige situationer; i nuancerede domæner som sprog kan ortogonale vektorer stadig dele subtile semantiske relationer, som metrikken ikke opfanger. Metrikkens afhængighed af korrekt normalisering betyder, at forkert skalerede data kan forvride resultater, og organisationer skal sikre ensartet forbehandling af alle vektorer i deres systemer. Endelig kan cosinuslighed alene være utilstrækkelig til komplekse lighedsvurderinger; kombination med andre metrikker og domænespecifikke valideringsregler giver ofte mere robuste resultater.
Rollen af cosinuslighed i AI-systemer udvikler sig løbende, i takt med at embedding-modeller bliver mere sofistikerede og vektorbaserede arkitekturer dominerer maskinlæring. Fremvoksende tendenser omfatter integration af cosinuslighed med hybride søgemetoder, der kombinerer vektorligning med traditionel fuldtekstsøgning, så systemer kan udnytte både semantisk forståelse og søgeords-match. Multimodale embeddings—der repræsenterer tekst, billeder, lyd og video i et fælles vektorrum—benytter i stigende grad cosinuslighed til at måle tværmodalle relationer, hvilket muliggør applikationer som billede-til-tekst-søgning og videoanalyse. Udviklingen af mere effektive approksimative nærmeste-nabo-algoritmer som DiskANN og HNSW forbedrer fortsat skalerbarheden af cosinuslighedssøgninger, så realtids semantisk søgning bliver mulig i hidtil uset skala. Kvantiseringsteknikker, der reducerer vektordimensionalitet, mens cosinuslighed-relationer bevares, muliggør udrulning af lighedssøgning i stor skala på edge-enheder og i ressourcebegrænsede miljøer. I forbindelse med AI-overvågning og brand tracking bliver cosinuslighed stadig vigtigere, efterhånden som organisationer søger at forstå, hvordan AI-systemer som ChatGPT, Perplexity, Claude og Google AI Overviews refererer og citerer deres indhold. Fremtidige udviklinger kan omfatte adaptive cosinuslighedsmetrikker, der tilpasser deres adfærd efter domænespecifikke karakteristika, og integration med forklaringsrammer, der hjælper brugere med at forstå, hvorfor bestemte vektorer anses for lignende. Efterhånden som vektordatabaser modnes og bliver standardinfrastruktur for AI-applikationer, vil cosinuslighed sandsynligvis forblive den dominerende metrik for semantiske sammenligninger, selvom den kan suppleres af domænespecifikke lighedsmål, der er tilpasset særlige applikationer og brugsscenarier.
For platforme som AmICited, der sporer brand- og domænementioner på tværs af AI-systemer, fungerer cosinuslighed som et centralt teknisk fundament. Når man overvåger, hvordan ChatGPT, Perplexity, Google AI Overviews og Claude refererer til specifikke domæner eller brands, muliggør cosinuslighed præcis måling af semantisk relevans mellem brugerforespørgsler og AI-svar. Ved at konvertere brandmentions, domæne-URL’er og forespørgselsindhold til vektorembeddings kan cosinuslighed afgøre, om et AI-svar faktisk citerer eller refererer til et brand, eller blot nævner relaterede begreber. Denne evne er afgørende for organisationer, der vil forstå deres synlighed i AI-genereret indhold og spore, hvordan deres intellektuelle ejendom bliver tilskrevet eller citeret af AI-systemer. Metrikkens effektivitet gør den praktisk til realtidsovervågning af millioner af AI-interaktioner, så organisationer kan modtage øjeblikkelige advarsler, når deres indhold refereres. Derudover muliggør cosinuslighed komparativ analyse—organisationer kan ikke kun spore, om de nævnes, men også hvordan deres nævnelsesfrekvens og relevans sammenlignes med konkurrenter, hvilket giver konkurrenceintelligens om AI-systemernes adfærd og indholdskilder.
En cosinuslighedsscore på 1 angiver, at to vektorer peger i præcis samme retning, hvilket betyder, at de er fuldstændig ens. En score på 0 betyder, at vektorerne er ortogonale (vinkelrette), hvilket indikerer ingen retningsmæssig relation eller lighed. En score på -1 indikerer, at vektorerne peger i præcis modsatte retninger, hvilket repræsenterer fuldstændig ulighed. I praktiske NLP-applikationer indikerer scorer tættere på 1 semantisk lignende tekster, mens scorer nær 0 antyder ikke-relateret indhold.
Cosinuslighed foretrækkes til tekst-embeddings, fordi den måler vinklen mellem vektorer frem for deres absolutte afstand, hvilket gør den ufølsom over for vektorens størrelse. Dette er afgørende for NLP, fordi dokumentlængde ikke bør påvirke semantisk lighed—en kort forespørgsel og en lang artikel kan være lige relevante. Euklidisk afstand er derimod følsom over for størrelse og fungerer dårligt i højdimensionelle rum, hvor vektorer har tendens til at konvergere. Cosinuslighed er også mere beregningseffektiv og naturligt begrænset mellem -1 og 1, hvilket forhindrer overflow-problemer.
I RAG-systemer driver cosinuslighed udtrækningsfasen ved at sammenligne forespørgselsembeddings med dokumentembeddings i en vektordatabase. Når en bruger indsender en forespørgsel, konverteres den til en vektor ved hjælp af samme embedding-model som de lagrede dokumenter. Cosinuslighed rangerer derefter dokumenterne efter relevans, hvor højere scorer indikerer bedre match. De højest rangerede dokumenter hentes og sendes til LLM'en som kontekst, hvilket muliggør mere præcise og faktuelt funderede svar. Denne proces gør det muligt for RAG-systemer at overvinde LLM-begrænsninger som forældet viden og hallucinationer.
Cosinuslighed har flere begrænsninger: den er udefineret, når vektorer har nulstørrelse, hvilket kræver forbehandling for at fjerne nullvektorer. Den kan give vildledende høje lighedsscorer for retningsorienterede men semantisk ikke-relaterede vektorer, især med dårligt trænede embeddings. Metrikken er også symmetrisk, hvilket betyder, at den ikke kan skelne rækkefølgen af sammenligning, hvilket kan være problematisk i visse applikationer. Desuden indikerer en lighedsscore på 0 ikke altid fuldstændig ulighed i virkelige kontekster, især i nuancerede domæner som sprog, hvor ortogonale vektorer stadig kan dele semantiske relationer.
Cosinuslighed beregnes med formlen: (A · B) / (||A|| × ||B||), hvor A · B er prikproduktet af vektorerne A og B, og ||A|| og ||B|| er deres størrelser (euklidiske normer). Prikproduktet beregnes ved at multiplicere tilsvarende vektorkomponenter og summere resultaterne. Størrelsen af en vektor er kvadratroden af summen af dets kvadrerede komponenter. Denne formel giver en normaliseret score mellem -1 og 1, hvilket gør den uafhængig af vektorlængde og velegnet til at sammenligne vektorer af forskellig størrelse.
I AI-overvågningsplatforme som AmICited er cosinuslighed afgørende for at spore brand- og domænementioner på tværs af AI-systemer som ChatGPT, Perplexity og Google AI Overviews. Ved at konvertere brandmentions og forespørgsler til vektorembeddings måler cosinuslighed, hvor tæt AI-genererede svar stemmer overens med det overvågede indhold. Dette gør det muligt for organisationer at overvåge, om deres domæner optræder i AI-svar, vurdere semantisk relevans af mentions og spore, hvordan AI-systemer refererer til deres indhold sammenlignet med konkurrenter. Metrikkens effektivitet gør den praktisk til realtidsmonitorering af millioner af AI-interaktioner.
Store AI-platforme og værktøjer, der udnytter cosinuslighed, inkluderer OpenAI's embedding-modeller, Googles semantiske søgealgoritmer, Perplexitys svargenereringssystem og Claudes udtrækningsmekanismer. Vektordatabaser som Pinecone, Weaviate og Milvus bruger cosinuslighed som deres primære lighedsmetrik. Open source-biblioteker som Scikit-learn, TensorFlow, PyTorch og NumPy tilbyder indbyggede funktioner til cosinuslighed. PostgreSQL med pgvector-udvidelsen muliggør cosinuslighedsberegninger i stor skala. Disse værktøjer driver tilsammen anbefalingssystemer, chatbots, semantiske søgemaskiner og RAG-applikationer på tværs af AI-økosystemet.
Begynd at spore, hvordan AI-chatbots nævner dit brand på tværs af ChatGPT, Perplexity og andre platforme. Få handlingsrettede indsigter til at forbedre din AI-tilstedeværelse.

Synlighedsscore måler søge-nærvær ved at beregne estimerede klik fra organiske placeringer. Lær hvordan denne metrik fungerer, dens beregningsmetoder, og hvorfo...

Semantisk lighed måler betydningsbaseret relaterethed mellem tekster ved hjælp af embeddings og afstandsmetrikker. Uundværlig til AI-overvågning, indholdsmatchn...

Lær hvad et AI Synlighedsindeks er, hvordan det kombinerer citeringsrate, placering, stemning og rækkeviddemålinger, og hvorfor det er vigtigt for brand synligh...