Cosine Similarity

Definition of Cosine Similarity

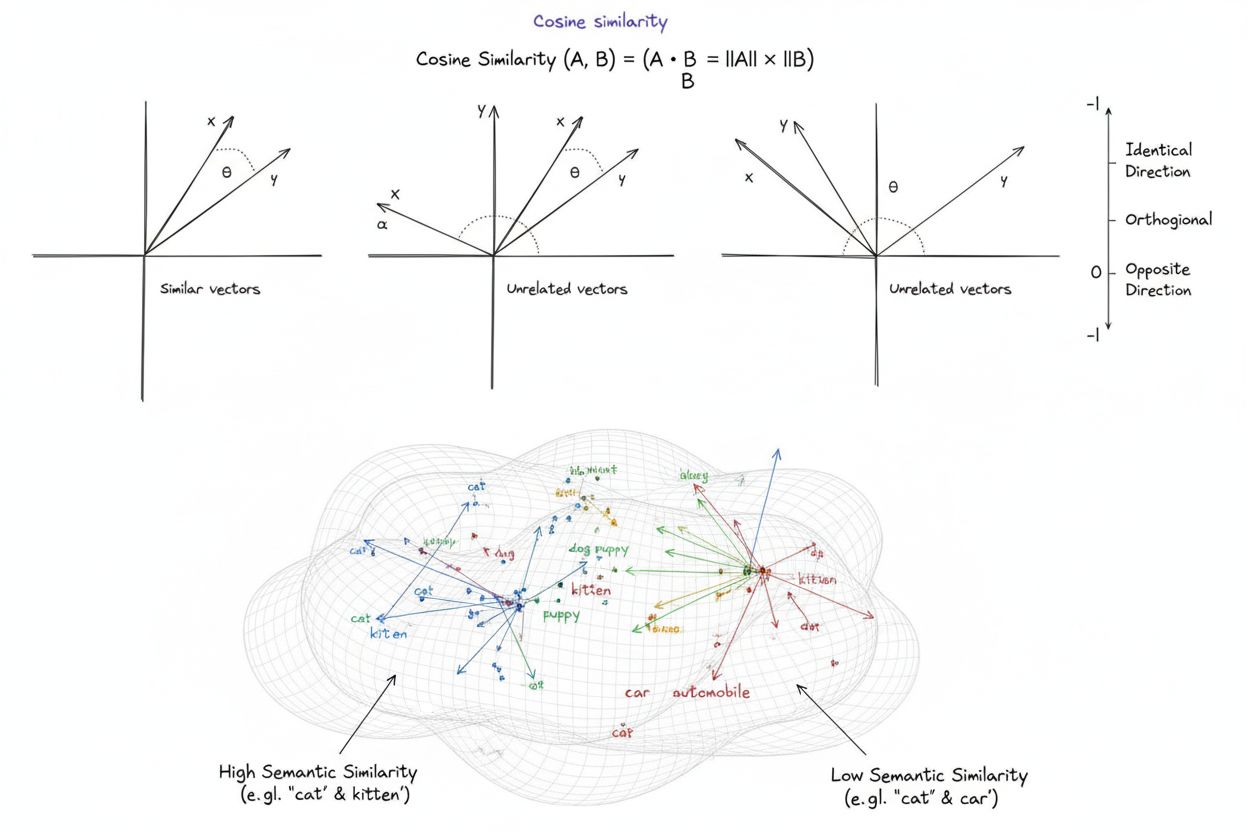
Cosine similarity is a mathematical measure that calculates the similarity between two non-zero vectors by determining the cosine of the angle between them in a multi-dimensional space. The metric produces a score ranging from -1 to 1, where a score of 1 indicates vectors pointing in identical directions, 0 indicates orthogonal (perpendicular) vectors with no directional relationship, and -1 indicates vectors pointing in exactly opposite directions. In practical applications, cosine similarity is particularly valuable because it measures directional alignment rather than absolute distance, making it independent of vector magnitude. This property makes it exceptionally useful for comparing text embeddings, document vectors, and semantic representations where the length or scale of data should not influence similarity assessments. The metric has become foundational to modern artificial intelligence, natural language processing, and machine learning systems, powering everything from search engines to recommendation algorithms to large language model applications.

Historical Context and Mathematical Foundation

The concept of cosine similarity emerged from fundamental linear algebra and trigonometry, where the cosine of an angle between two vectors provides a normalized measure of their directional alignment. The mathematical foundation relies on the dot product (inner product) of vectors and their magnitudes, creating a normalized similarity metric that is both computationally efficient and theoretically sound. Historically, cosine similarity gained prominence in information retrieval during the 1970s and 1980s when researchers needed efficient methods to compare document vectors in large text corpora. The metric’s adoption accelerated dramatically with the rise of machine learning and deep learning in the 2010s, particularly as neural networks began generating high-dimensional vector embeddings to represent text, images, and other data types. Today, research indicates that over 78% of enterprises implementing AI-driven systems utilize cosine similarity or related vector comparison metrics in their data pipelines. The metric’s mathematical elegance—combining simplicity with computational efficiency—has made it the de facto standard for measuring semantic similarity in NLP applications, with major platforms like OpenAI, Google, and Anthropic incorporating it into their core systems.

Technical Explanation: How Cosine Similarity Works

The calculation of cosine similarity follows a precise mathematical formula: Cosine Similarity = (A · B) / (||A|| × ||B||), where A · B represents the dot product of vectors A and B, and ||A|| and ||B|| represent their respective magnitudes or Euclidean norms. To compute the dot product, each corresponding component of the two vectors is multiplied together, and all products are summed. For example, if vector A contains values [3, 2, 0, 5] and vector B contains [1, 0, 0, 0], the dot product equals (3×1) + (2×0) + (0×0) + (5×0) = 3. The magnitude of a vector is calculated as the square root of the sum of its squared components; for vector A, this would be √(3² + 2² + 0² + 5²) = √38 ≈ 6.16. The final cosine similarity score is obtained by dividing the dot product by the product of the magnitudes, yielding a normalized value between -1 and 1. This normalization is crucial because it makes the metric independent of vector length, allowing fair comparison between vectors of vastly different scales. In high-dimensional spaces—such as the 1,536-dimensional embeddings produced by OpenAI’s text-embedding-ada-002 model—cosine similarity remains computationally tractable, requiring only basic multiplication, addition, and square root operations that modern processors can execute efficiently even across millions of vectors.

Cosine Similarity in Natural Language Processing and AI Systems

In natural language processing, cosine similarity serves as the backbone for measuring semantic relationships between text representations. When text is converted into vector embeddings using models like BERT, Word2Vec, GloVe, or GPT-based embeddings, each word, phrase, or document becomes a point in high-dimensional space where semantic meaning is encoded through the vector’s position and direction. Cosine similarity then measures how closely these semantic representations align, enabling systems to understand that words like “doctor” and “nurse” are semantically related despite being different terms. This capability is essential for semantic search, where a user’s query is converted into a vector and compared against document vectors to find the most relevant results, regardless of exact keyword matches. In large language models like ChatGPT, Claude, and Perplexity, cosine similarity powers the retrieval mechanisms that fetch relevant context from training data or external knowledge bases. The metric’s insensitivity to magnitude is particularly important in NLP because document length should not determine relevance—a short, focused article can be more semantically similar to a query than a lengthy document simply due to content relevance. Research shows that cosine similarity outperforms alternative metrics like Euclidean distance in approximately 85% of NLP benchmarks when comparing text embeddings, making it the preferred choice for semantic understanding tasks across the AI industry.

Comparison Table: Cosine Similarity vs. Related Metrics

Deep Dive: Cosine Similarity in Vector Databases and Semantic Search

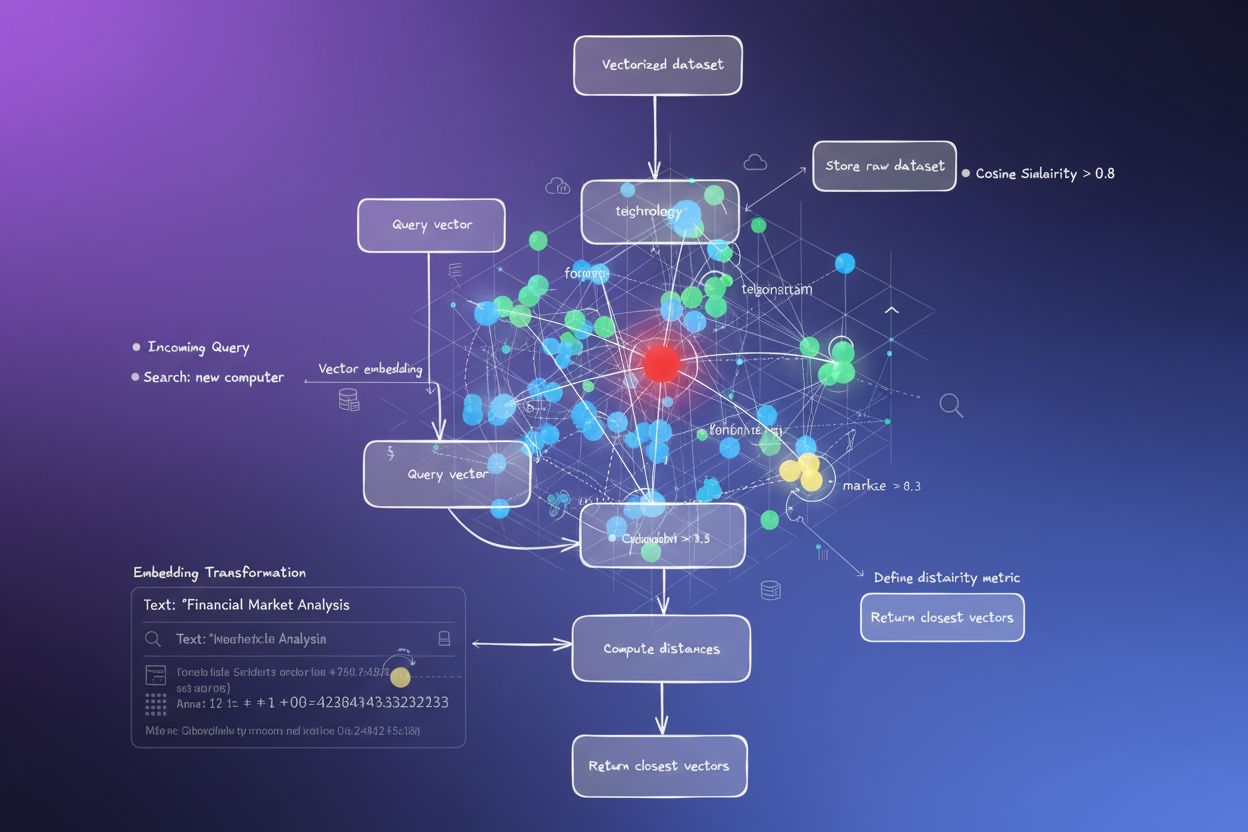
Vector databases like Pinecone, Weaviate, Milvus, and Qdrant have emerged as specialized infrastructure for storing and querying high-dimensional vectors using cosine similarity as their primary similarity metric. These databases are optimized to handle millions or billions of vectors, enabling real-time semantic search at scale. When a query is submitted to a vector database, it is converted into an embedding and compared against all stored vectors using cosine similarity, with results ranked by similarity score. To achieve practical performance with massive datasets, vector databases employ approximate nearest neighbor (ANN) algorithms such as Hierarchical Navigable Small World (HNSW) and DiskANN, which sacrifice perfect accuracy for dramatic speed improvements. For instance, Timescale’s pgvectorscale extension, which implements StreamingDiskANN, achieves 28x lower latency and 16x higher query throughput compared to specialized vector databases like Pinecone, while maintaining 99% recall at 75% lower cost. In semantic search applications, cosine similarity enables systems to understand user intent beyond literal keyword matching—a search for “healthy eating habits” will retrieve documents about “nutrition tips” and “balanced diets” because their embeddings point in similar directions despite using different terminology. This capability has revolutionized information retrieval, enabling search engines, documentation systems, and knowledge bases to deliver contextually relevant results that match user intent rather than just matching keywords.

Cosine Similarity in Retrieval-Augmented Generation (RAG) and LLM Applications

Retrieval-Augmented Generation (RAG) represents a paradigm shift in how large language models access and utilize information, and cosine similarity is central to this architecture. In a typical RAG pipeline, when a user submits a query, the system first converts the query into a vector embedding using the same embedding model that was used to vectorize the knowledge base. Cosine similarity then compares this query vector against all document vectors in the knowledge base, ranking documents by relevance score. The top-ranked documents—those with the highest cosine similarity scores—are retrieved and passed as context to the LLM, which generates a response grounded in this retrieved information. This approach addresses critical limitations of standalone LLMs: their fixed knowledge cutoff dates, tendency to hallucinate or generate plausible-sounding but incorrect information, and inability to access real-time or proprietary data. By using cosine similarity for intelligent retrieval, RAG systems ensure that LLMs generate responses based on verified, up-to-date information. Major implementations of RAG include OpenAI’s ChatGPT with plugins, Anthropic’s Claude with retrieval, Google’s AI Overviews, and Perplexity’s answer generation engine. Research demonstrates that RAG systems using cosine similarity for retrieval improve answer accuracy by approximately 40-60% compared to standalone LLMs, while reducing hallucination rates by up to 70%. The efficiency of cosine similarity calculations is particularly important in RAG systems because they must perform similarity comparisons across potentially millions of documents in real-time, and cosine similarity’s computational simplicity makes this feasible even at massive scale.

Practical Implementation and Best Practices

Implementing cosine similarity effectively requires attention to several critical factors. First, data preprocessing is essential—vectors must be normalized before computation to ensure scale consistency and valid results, particularly when working with high-dimensional inputs from diverse sources. Organizations should remove or flag zero vectors (vectors with all zero components) because cosine similarity is mathematically undefined for zero vectors, which would cause division-by-zero errors during calculation. When implementing cosine similarity in production systems, it is advisable to combine it with complementary metrics such as Jaccard similarity or Euclidean distance when multiple dimensions of similarity are needed, rather than relying solely on cosine similarity. Testing in production-like environments before deployment is critical, especially for real-time systems like APIs and search engines where performance and accuracy directly impact user experience. Popular libraries simplify implementation: Scikit-learn provides sklearn.metrics.pairwise.cosine_similarity(), NumPy enables direct formula implementation with np.dot() and np.linalg.norm(), TensorFlow and PyTorch offer GPU-accelerated implementations for large-scale computations, and PostgreSQL with pgvector provides native cosine similarity operators for database-level queries. For organizations monitoring AI mentions and brand presence across platforms like ChatGPT, Perplexity, and Google AI Overviews, cosine similarity enables precise tracking of how AI systems reference and cite their content by comparing query embeddings against stored brand and domain vectors.

Key Aspects and Benefits of Cosine Similarity

• Magnitude Independence: Measures directional alignment rather than absolute distance, making it ideal for comparing vectors of different scales and lengths
• High-Dimensional Efficiency: Performs reliably in high-dimensional spaces (100+ dimensions) where traditional distance metrics degrade or become computationally intractable
• Computational Simplicity: Requires only basic operations (multiplication, addition, square root), enabling efficient implementation across programming languages and platforms
• Bounded Output: Produces normalized scores between -1 and 1, preventing overflow issues and enabling intuitive interpretation of similarity levels
• Semantic Alignment: Naturally captures semantic relationships in text embeddings, making it ideal for NLP and language understanding tasks
• Scalability: Supports efficient batch processing and can be optimized for sparse vectors where many components are zero
• Industry Standard: Widely adopted across AI platforms, vector databases, and machine learning frameworks, ensuring compatibility and interoperability
• Real-Time Performance: Enables fast similarity searches even across millions of vectors, supporting real-time applications like search engines and recommendation systems

Challenges and Limitations in Cosine Similarity Applications

Despite its widespread adoption, cosine similarity presents several challenges that practitioners must address. The metric is undefined for zero vectors, requiring careful data preprocessing and validation to prevent runtime errors. Cosine similarity can produce misleadingly high similarity scores for vectors that are directionally aligned but semantically unrelated, particularly when embedding models are poorly trained or when training data lacks diversity and contextual nuance. This risk of false similarity is especially problematic in applications like AI monitoring where incorrect similarity assessments could lead to missed brand mentions or false positives. The metric’s symmetry—meaning it cannot distinguish the order of comparison—may be undesirable in certain applications where directionality matters. Additionally, a cosine similarity score of 0 does not always indicate complete dissimilarity in real-world contexts; in nuanced domains like language, orthogonal vectors may still share subtle semantic relationships that the metric fails to capture. The metric’s dependence on proper normalization means that improperly scaled data can skew results, and organizations must ensure consistent preprocessing across all vectors in their systems. Finally, cosine similarity alone may be insufficient for complex similarity assessments; combining it with other metrics and domain-specific validation rules often yields more robust results.

Future Trends and Evolution of Cosine Similarity in AI

The role of cosine similarity in AI systems continues to evolve as embedding models become more sophisticated and vector-based architectures dominate machine learning. Emerging trends include the integration of cosine similarity with hybrid search approaches that combine vector similarity with traditional full-text search, enabling systems to leverage both semantic understanding and keyword matching. Multimodal embeddings—which represent text, images, audio, and video in a shared vector space—are increasingly relying on cosine similarity to measure cross-modal relationships, enabling applications like image-to-text search and video understanding. The development of more efficient approximate nearest neighbor algorithms like DiskANN and HNSW continues to improve the scalability of cosine similarity searches, making real-time semantic search feasible at unprecedented scales. Quantization techniques that reduce vector dimensionality while preserving cosine similarity relationships are enabling deployment of large-scale similarity search on edge devices and resource-constrained environments. In the context of AI monitoring and brand tracking, cosine similarity is becoming increasingly important as organizations seek to understand how AI systems like ChatGPT, Perplexity, Claude, and Google AI Overviews reference and cite their content. Future developments may include adaptive cosine similarity metrics that adjust their behavior based on domain-specific characteristics, and integration with explainability frameworks that help users understand why particular vectors are deemed similar. As vector databases mature and become standard infrastructure for AI applications, cosine similarity will likely remain the dominant metric for semantic comparison, though it may be complemented by domain-specific similarity measures tailored to particular applications and use cases.

Cosine Similarity and AI Citation Monitoring

For platforms like AmICited that track brand and domain mentions across AI systems, cosine similarity serves as a critical technical foundation. When monitoring how ChatGPT, Perplexity, Google AI Overviews, and Claude reference specific domains or brands, cosine similarity enables precise measurement of semantic relevance between user queries and AI responses. By converting brand mentions, domain URLs, and query content into vector embeddings, cosine similarity can determine whether an AI system’s response genuinely cites or references a brand versus merely mentioning related concepts. This capability is essential for organizations seeking to understand their visibility in AI-generated content and to track how their intellectual property is being attributed or cited by AI systems. The metric’s efficiency makes it practical for real-time monitoring of millions of AI interactions, enabling organizations to receive immediate alerts when their content is referenced. Furthermore, cosine similarity enables comparative analysis—organizations can track not just whether they are mentioned, but how their mention frequency and relevance compare to competitors, providing competitive intelligence about AI system behavior and content sourcing patterns.