Similaritatea cosinusului

Definiția similarității cosinusului

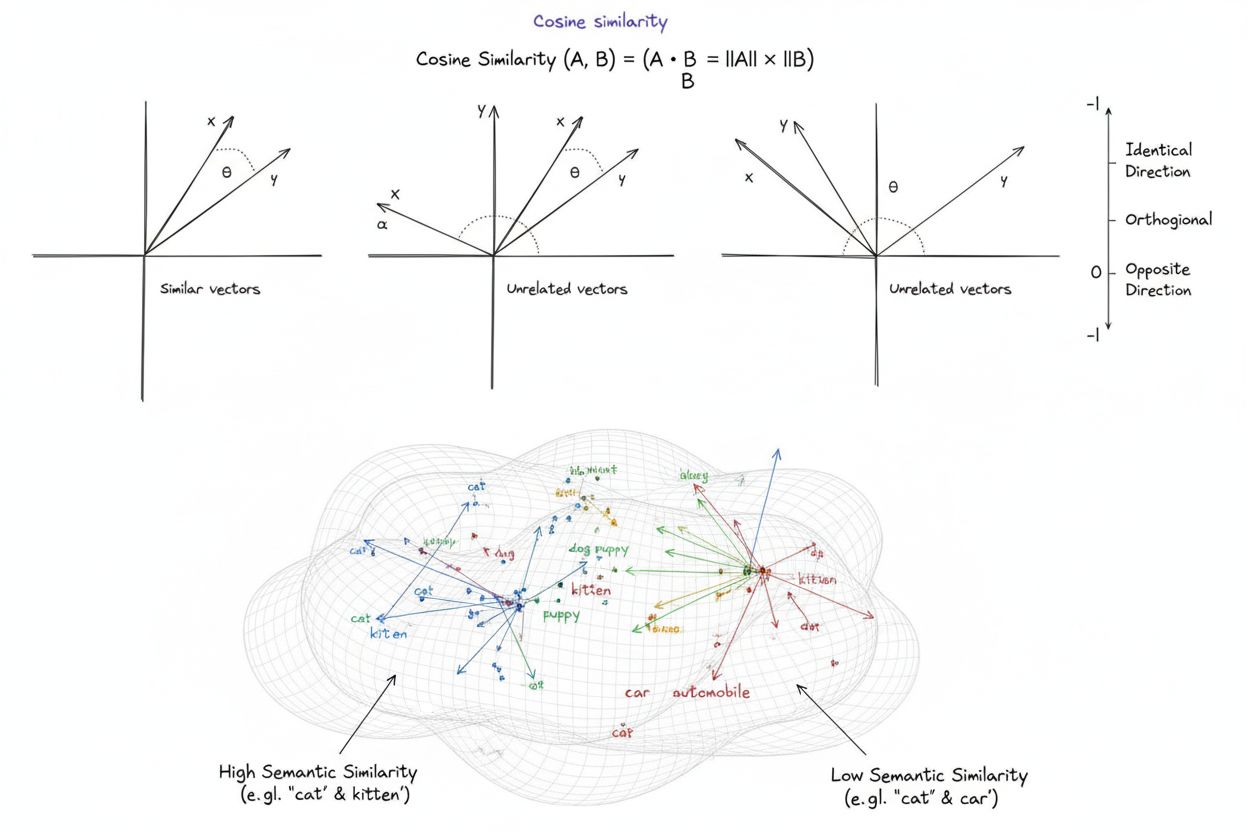
Similaritatea cosinusului este o măsură matematică ce calculează similaritatea dintre doi vectori nenuli determinând cosinusul unghiului dintre ei într-un spațiu multi-dimensional. Metrica produce un scor cuprins între -1 și 1, unde 1 indică vectori orientați în direcții identice, 0 indică vectori ortogonali (perpendiculare) fără relație direcțională, iar -1 indică vectori orientați exact în direcții opuse. În aplicațiile practice, similaritatea cosinusului este deosebit de valoroasă deoarece măsoară alinierea direcțională, nu distanța absolută, făcând-o independentă de magnitudinea vectorului. Această proprietate o face extrem de utilă pentru compararea embedding-urilor de text, a vectorilor de documente și a reprezentărilor semantice unde lungimea sau scara datelor nu ar trebui să influențeze evaluarea similarității. Metrica a devenit fundamentală pentru sistemele moderne de inteligență artificială, procesare a limbajului natural și învățare automată, alimentând de la motoare de căutare la algoritmi de recomandare și aplicații de tip large language model.

Context istoric și fundație matematică

Conceptul de similaritate a cosinusului provine din algebra liniară fundamentală și trigonometrie, unde cosinusul unghiului dintre doi vectori oferă o măsură normalizată a alinierii lor direcționale. Fundamentul matematic se bazează pe produsul scalar (produs intern) al vectorilor și pe magnitudinea acestora, creând o metrică de similaritate normalizată, atât eficientă computațional, cât și solidă teoretic. Istoric, similaritatea cosinusului a câștigat notorietate în domeniul regăsirii informațiilor în anii 1970 și 1980, când cercetătorii au avut nevoie de metode eficiente pentru a compara vectorii de documente în corpusuri mari de texte. Adoptarea metricii a accelerat dramatic odată cu ascensiunea învățării automate și a învățării profunde în anii 2010, în special pe măsură ce rețelele neuronale au început să genereze embedding-uri vectoriale de înaltă dimensiune pentru a reprezenta texte, imagini și alte tipuri de date. Astăzi, cercetările indică faptul că peste 78% dintre companiile care implementează sisteme bazate pe AI utilizează similaritatea cosinusului sau metrici de comparare a vectorilor în fluxurile lor de date. Eleganța matematică a metricii—combinând simplitatea cu eficiența computațională—a făcut-o standardul de facto pentru măsurarea similarității semantice în aplicațiile de NLP, mari platforme precum OpenAI, Google și Anthropic integrând-o în sistemele lor de bază.

Explicație tehnică: Cum funcționează similaritatea cosinusului

Calculul similarității cosinusului urmează o formulă matematică precisă: Similaritatea cosinusului = (A · B) / (||A|| × ||B||), unde A · B reprezintă produsul scalar al vectorilor A și B, iar ||A|| și ||B|| reprezintă magnitudinile sau normele lor Euclidiene. Pentru a calcula produsul scalar, fiecare componentă corespunzătoare a celor doi vectori se înmulțește, iar rezultatele se însumează. De exemplu, dacă vectorul A are valorile [3, 2, 0, 5] și vectorul B are [1, 0, 0, 0], produsul scalar va fi (3×1) + (2×0) + (0×0) + (5×0) = 3. Magnitudinea unui vector se calculează ca rădăcina pătrată a sumei componentelor sale ridicate la pătrat; pentru vectorul A, aceasta ar fi √(3² + 2² + 0² + 5²) = √38 ≈ 6.16. Scorul final de similaritate cosinus se obține împărțind produsul scalar la produsul magnitudinilor, rezultând o valoare normalizată între -1 și 1. Această normalizare este esențială deoarece face metrica independentă de lungimea vectorilor, permițând compararea echitabilă a vectorilor cu scări foarte diferite. În spații de înaltă dimensiune—precum embedding-urile cu 1.536 dimensiuni produse de modelul text-embedding-ada-002 al OpenAI—similaritatea cosinusului rămâne abordabilă computațional, necesitând doar operații elementare de înmulțire, adunare și rădăcină pătrată pe care procesoarele moderne le pot executa eficient chiar și asupra a milioane de vectori.

Similaritatea cosinusului în procesarea limbajului natural și sistemele AI

În procesarea limbajului natural, similaritatea cosinusului stă la baza măsurării relațiilor semantice dintre reprezentările textului. Când textul este convertit în embedding-uri vectoriale folosind modele precum BERT, Word2Vec, GloVe sau embedding-uri bazate pe GPT, fiecare cuvânt, expresie sau document devine un punct într-un spațiu de înaltă dimensiune în care semnificația semantică este codificată prin poziția și direcția vectorului. Similaritatea cosinusului măsoară cât de apropiate sunt aceste reprezentări semantice, permițând sistemelor să înțeleagă că termeni precum „doctor” și „asistentă” sunt înrudiți semantic, deși sunt termeni diferiți. Această capacitate este esențială pentru căutarea semantică, unde interogarea unui utilizator este convertită într-un vector și comparată cu vectorii de document pentru a găsi cele mai relevante rezultate, indiferent de potrivirile exacte ale cuvintelor-cheie. În modele lingvistice mari precum ChatGPT, Claude și Perplexity, similaritatea cosinusului alimentează mecanismele de regăsire care extrag context relevant din datele de antrenament sau baze de cunoștințe externe. Insensibilitatea metricii la magnitudine este deosebit de importantă în NLP deoarece lungimea documentului nu trebuie să determine relevanța—un articol scurt și concentrat poate fi mai similar semantic cu o interogare decât un document lung, doar datorită relevanței conținutului. Studiile arată că similaritatea cosinusului depășește metrici alternative precum distanța Euclidiană în aproximativ 85% dintre benchmark-urile NLP la compararea embedding-urilor de text, devenind astfel alegerea preferată pentru sarcinile de înțelegere semantică din industria AI.

Tabel comparativ: Similaritatea cosinusului vs. metrici înrudite

Analiză detaliată: Similaritatea cosinusului în baze de date vectoriale și căutare semantică

Baze de date vectoriale precum Pinecone, Weaviate, Milvus și Qdrant au apărut ca infrastructură specializată pentru stocarea și interogarea vectorilor de înaltă dimensiune folosind similaritatea cosinusului ca metrică principală. Aceste baze de date sunt optimizate pentru a gestiona milioane sau miliarde de vectori, permițând căutare semantică în timp real la scară mare. Când o interogare este trimisă către o bază de date vectorială, aceasta este convertită într-un embedding și comparată cu toți vectorii stocați folosind similaritatea cosinusului, rezultatele fiind ordonate după scorul de similaritate. Pentru a obține performanță practică cu seturi de date masive, baze de date vectoriale utilizează algoritmi approximate nearest neighbor (ANN) precum Hierarchical Navigable Small World (HNSW) și DiskANN, care sacrifică acuratețea perfectă pentru îmbunătățiri dramatice de viteză. De exemplu, extensia pgvectorscale de la Timescale, ce implementează StreamingDiskANN, obține de 28 ori latență mai mică și de 16 ori randament de interogare mai mare comparativ cu baze vectoriale specializate precum Pinecone, menținând 99% recall la costuri cu 75% mai mici. În aplicațiile de căutare semantică, similaritatea cosinusului permite sistemelor să înțeleagă intenția utilizatorului dincolo de potrivirile literale ale cuvintelor-cheie—o căutare pentru „obiceiuri alimentare sănătoase” va regăsi documente despre „sfaturi nutriționale” și „diete echilibrate” deoarece embedding-urile lor sunt orientate în direcții similare, chiar dacă folosesc terminologie diferită. Această capacitate a revoluționat regăsirea informațiilor, permițând motoarelor de căutare, sistemelor de documentație și bazelor de cunoștințe să ofere rezultate relevant contextuale care să corespundă intenției utilizatorului, nu doar cuvintelor-cheie.

Similaritatea cosinusului în Retrieval-Augmented Generation (RAG) și aplicații LLM

Retrieval-Augmented Generation (RAG) reprezintă o schimbare de paradigmă în modul în care modelele lingvistice mari accesează și utilizează informația, iar similaritatea cosinusului este centrală în această arhitectură. Într-un flux tipic RAG, când un utilizator trimite o interogare, sistemul convertește mai întâi această interogare într-un embedding vectorial folosind același model de embedding folosit pentru baza de cunoștințe. Similaritatea cosinusului compară acest vector de interogare cu toți vectorii de document din baza de cunoștințe, ordonând documentele după scorul de relevanță. Documentele cel mai bine clasate—cele cu cele mai mari scoruri de similaritate cosinus—sunt regăsite și transmise ca context către LLM, care generează un răspuns fundamentat pe aceste informații. Această abordare rezolvă limitări critice ale LLM-urilor de sine stătătoare: date de tăiere a cunoașterii fixe, tendința de halucinații sau generare de informații plauzibile dar incorecte și incapacitatea de a accesa date în timp real sau proprietare. Folosind similaritatea cosinusului pentru regăsire inteligentă, sistemele RAG asigură că LLM-urile generează răspunsuri pe baza unor informații verificate și actualizate. Implementări majore ale RAG includ ChatGPT de la OpenAI cu plugin-uri, Claude de la Anthropic cu retrieval, Google AI Overviews și motorul de generare de răspunsuri Perplexity. Studiile arată că sistemele RAG care folosesc similaritatea cosinusului pentru regăsire cresc acuratețea răspunsurilor cu aproximativ 40-60% față de LLM-urile de sine stătătoare, reducând rata halucinațiilor cu până la 70%. Eficiența calculelor de similaritate cosinus este deosebit de importantă în sistemele RAG deoarece acestea trebuie să efectueze comparații de similaritate pe milioane de documente în timp real, iar simplitatea computațională a metricii face acest lucru fezabil chiar și la scară masivă.

Implementare practică și bune practici

Implementarea eficientă a similarității cosinusului necesită atenție la câțiva factori critici. În primul rând, preprocesarea datelor este esențială—vectorii trebuie normalizați înainte de calcul pentru a asigura consistența scării și rezultate valide, în special când se lucrează cu intrări de înaltă dimensiune din surse diverse. Organizațiile ar trebui să elimine sau să marcheze vectorii zero (vectori cu toate componentele zero) deoarece similaritatea cosinusului este nedefinită matematic pentru aceștia, ceea ce ar duce la erori de tip dividere cu zero în timpul calculului. La implementarea similarității cosinusului în sisteme de producție, este recomandat să fie combinată cu metrici complementare precum similaritatea Jaccard sau distanța Euclidiană când sunt necesare mai multe dimensiuni de similaritate, nu doar similaritatea cosinusului. Testarea în medii apropiate de producție înainte de lansare este crucială, mai ales pentru sisteme în timp real precum API-uri și motoare de căutare unde performanța și acuratețea au impact direct asupra experienței utilizatorului. Biblioteci populare simplifică implementarea: Scikit-learn oferă sklearn.metrics.pairwise.cosine_similarity(), NumPy permite implementarea directă a formulei cu np.dot() și np.linalg.norm(), TensorFlow și PyTorch oferă implementări accelerate GPU pentru calcule la scară mare, iar PostgreSQL cu pgvector oferă operatori nativi de similaritate cosinus pentru interogări la nivel de bază de date. Pentru organizațiile care monitorizează mențiuni AI și prezența brandului pe platforme precum ChatGPT, Perplexity și Google AI Overviews, similaritatea cosinusului permite urmărirea precisă a modului în care sistemele AI fac referire și citează conținutul lor, comparând embedding-urile interogărilor cu vectorii de brand și domeniu stocați.

Aspecte cheie și beneficii ale similarității cosinusului

• Independență față de magnitudine: Măsoară alinierea direcțională, nu distanța absolută, fiind ideală pentru compararea vectorilor de scări și lungimi diferite
• Eficiență în spații de înaltă dimensiune: Funcționează fiabil în spații cu peste 100 de dimensiuni, unde metricele tradiționale devin ineficiente sau imposibile computațional
• Simplitate computațională: Necesită doar operații de bază (înmulțire, adunare, rădăcină pătrată), permițând implementare eficientă pe orice limbaj sau platformă
• Rezultate încadrate: Produce scoruri normalizate între -1 și 1, prevenind overflow-ul și permițând interpretarea intuitivă a nivelurilor de similaritate
• Aliniere semantică: Surprinde în mod natural relațiile semantice în embedding-urile de text, fiind ideală pentru sarcinile NLP și de înțelegere a limbajului
• Scalabilitate: Suportă procesare eficientă în loturi și poate fi optimizată pentru vectori rari unde multe componente sunt zero
• Standard în industrie: Adoptată pe scară largă pe platforme AI, baze de date vectoriale și framework-uri de machine learning, asigurând compatibilitate și interoperabilitate
• Performanță în timp real: Permite căutări rapide de similaritate chiar pe milioane de vectori, susținând aplicații în timp real precum motoare de căutare și sisteme de recomandare

Provocări și limitări în aplicațiile similarității cosinusului

În ciuda adoptării extinse, similaritatea cosinusului prezintă mai multe provocări ce trebuie gestionate de practicieni. Metrica este nedefinită pentru vectorii zero, necesitând preprocesare și validare atentă a datelor pentru a preveni erorile la rulare. Similaritatea cosinusului poate produce scoruri de similaritate în mod înșelător ridicate pentru vectori care sunt aliniați direcțional, dar nesemnificativ similar semantic, mai ales când modelele de embedding sunt slab antrenate sau datele de antrenament nu includ diversitate și nuanță contextuală. Acest risc de similaritate falsă este problematic în special în aplicații precum monitorizarea AI, unde evaluări greșite pot duce la mențiuni de brand ratate sau la alarme false. Simetria metricii—adică nu distinge ordinea comparării—poate fi nedorită în anumite aplicații unde contează direcționalitatea. De asemenea, un scor de similaritate cosinus de 0 nu indică întotdeauna o disimilaritate completă în contexte reale; în domenii nuanțate precum limbajul, vectorii ortogonali pot împărtăși totuși relații semantice subtile pe care metrica nu le surprinde. Dependența metricii de normalizare corectă înseamnă că datele scalate necorespunzător pot distorsiona rezultatele, iar organizațiile trebuie să asigure preprocesare consistentă pentru toți vectorii din sistemele lor. În cele din urmă, similaritatea cosinusului singură poate fi insuficientă pentru evaluări complexe de similaritate; combinarea cu alte metrici și reguli de validare specifice domeniului oferă adesea rezultate mai robuste.

Tendințe viitoare și evoluția similarității cosinusului în AI

Rolul similarității cosinusului în sistemele AI continuă să evolueze pe măsură ce modelele de embedding devin tot mai sofisticate, iar arhitecturile bazate pe vectori domină învățarea automată. Tendințe emergente includ integrarea similarității cosinusului cu abordări hybrid search ce combină similaritatea vectorială cu căutarea full-text tradițională, permițând sistemelor să valorifice atât înțelegerea semantică, cât și potrivirea cuvintelor-cheie. Embedding-urile multimodale—care reprezintă texte, imagini, audio și video într-un spațiu vectorial comun—se bazează tot mai mult pe similaritatea cosinusului pentru a măsura relațiile cross-modal, permițând aplicații precum căutarea de imagini după text sau înțelegerea videoclipurilor. Dezvoltarea de algoritmi approximate nearest neighbor precum DiskANN și HNSW îmbunătățește continuu scalabilitatea căutărilor cu similaritatea cosinusului, făcând căutarea semantică în timp real posibilă la scări fără precedent. Tehnicile de cuantizare ce reduc dimensionalitatea vectorilor păstrând relațiile de similaritate cosinus permit implementarea căutării de similaritate la scară mare pe dispozitive edge sau în medii cu resurse limitate. În contextul monitorizării AI și urmărirea brandului, similaritatea cosinusului devine tot mai importantă pe măsură ce organizațiile doresc să înțeleagă cum sisteme precum ChatGPT, Perplexity, Claude și Google AI Overviews fac referire și citesc conținutul lor. Dezvoltări viitoare pot include metrici adaptive de similaritate cosinus ce își ajustează comportamentul în funcție de caracteristicile domeniului și integrarea cu framework-uri de explicabilitate care ajută utilizatorii să înțeleagă de ce anumiți vectori sunt considerați similari. Pe măsură ce baze de date vectoriale se maturizează și devin infrastructură standard pentru aplicațiile AI, similaritatea cosinusului va rămâne probabil metrica dominantă pentru compararea semantică, deși poate fi completată de măsuri de similaritate specifice domeniului, adaptate aplicațiilor și cazurilor particulare.

Similaritatea cosinusului și monitorizarea citărilor AI

Pentru platforme precum AmICited ce urmăresc mențiuni de brand și domeniu în sistemele AI, similaritatea cosinusului servește ca fundație tehnică esențială. La monitorizarea modului în care ChatGPT, Perplexity, Google AI Overviews și Claude fac referire la anumite domenii sau branduri, similaritatea cosinusului permite măsurarea precisă a relevanței semantice dintre interogările utilizatorilor și răspunsurile AI. Prin convertirea mențiunilor de brand, a URL-urilor de domeniu și a conținutului interogărilor în embedding-uri vectoriale, similaritatea cosinusului poate determina dacă un răspuns AI citează sau face referire cu adevărat la un brand sau doar menționează concepte înrudite. Această capacitate este esențială pentru organizațiile care doresc să își înțeleagă vizibilitatea în conținutul generat de AI și să urmărească modul în care proprietatea lor intelectuală este atribuită sau citată de aceste sisteme. Eficiența metricii o face practică pentru monitorizarea în timp real a milioane de interacțiuni AI, permițând organizațiilor să primească alerte imediate când conținutul lor este referențiat. Mai mult, similaritatea cosinusului permite analize comparative—organizațiile pot urmări nu doar dacă sunt menționate, ci și cât de des și cât de relevante sunt mențiunile comparativ cu competitorii, oferind informații competitive despre comportamentul sistemelor AI și tiparele de citare a conținutului.