
Semantisk Liktet
Semantisk likhet måler meningsbasert beslektethet mellom tekster ved hjelp av embeddinger og avstandsmål. Essensiell for AI-overvåkning, innholdsmatching og mer...
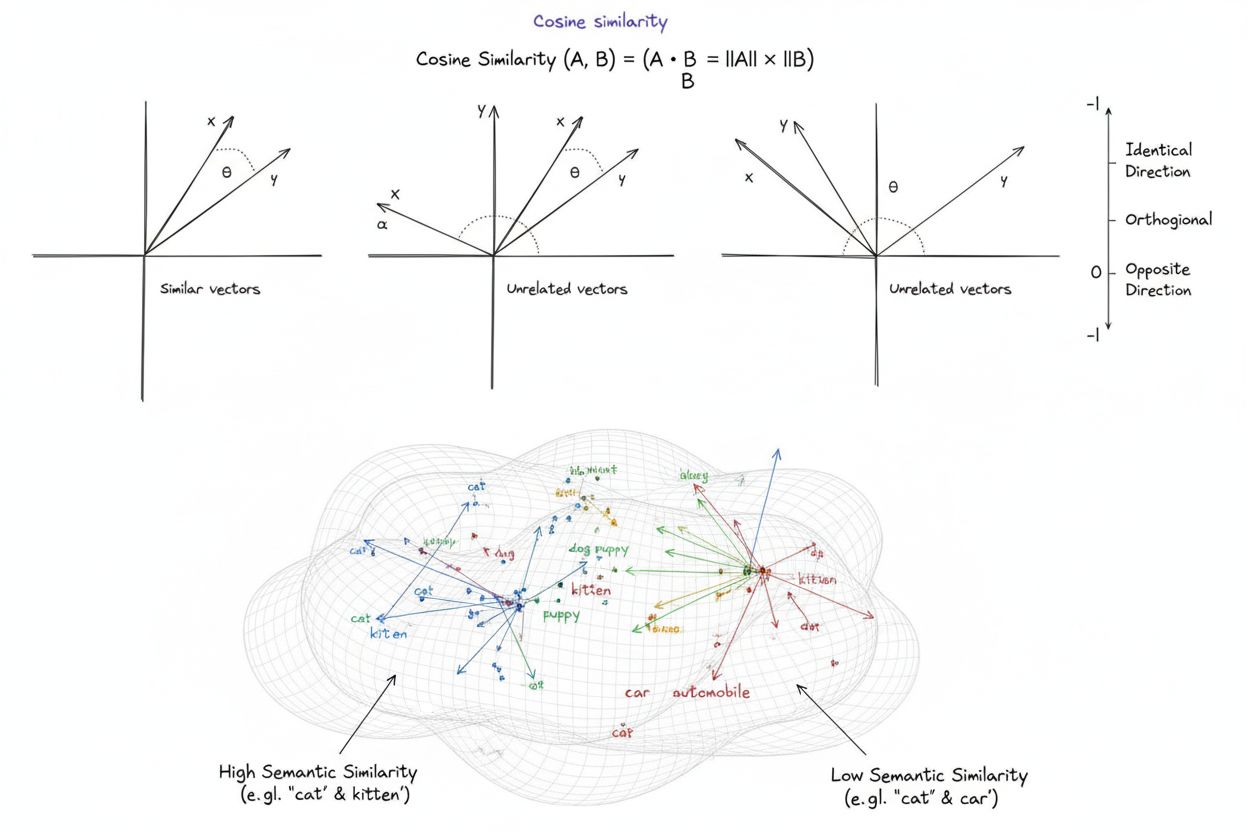
Cosinuslikhet er et matematisk mål som beregner likheten mellom to ikke-nulle vektorer ved å bestemme cosinus til vinkelen mellom dem, og gir en score fra -1 til 1. Det er mye brukt innen maskinlæring, naturlig språkbehandling og AI-systemer for å måle semantisk likhet mellom tekst-embeddinger og vektorrepresentasjoner, uavhengig av vektormagnitud.
Cosinuslikhet er et matematisk mål som beregner likheten mellom to ikke-nulle vektorer ved å bestemme cosinus til vinkelen mellom dem, og gir en score fra -1 til 1. Det er mye brukt innen maskinlæring, naturlig språkbehandling og AI-systemer for å måle semantisk likhet mellom tekst-embeddinger og vektorrepresentasjoner, uavhengig av vektormagnitud.
Cosinuslikhet er et matematisk mål som beregner likheten mellom to ikke-nulle vektorer ved å bestemme cosinus til vinkelen mellom dem i et flerdimensjonalt rom. Metrikken gir en score fra -1 til 1, der en score på 1 indikerer at vektorene peker i identiske retninger, 0 indikerer ortogonale (vinkelrette) vektorer uten retningsmessig relasjon, og -1 indikerer at vektorene peker i nøyaktig motsatte retninger. I praktiske applikasjoner er cosinuslikhet spesielt verdifull fordi den måler retningsmessig samsvar fremfor absolutt avstand, noe som gjør den uavhengig av vektormagnitud. Denne egenskapen gjør den svært nyttig for å sammenligne tekst-embeddinger, dokumentvektorer og semantiske representasjoner der lengde eller skala på data ikke skal påvirke likhetsvurderinger. Metrikken har blitt grunnleggende for moderne kunstig intelligens, naturlig språkbehandling og maskinlæringssystemer, og driver alt fra søkemotorer til anbefalingsalgoritmer og applikasjoner basert på store språkmodeller.
Konseptet cosinuslikhet oppsto fra grunnleggende lineær algebra og trigonometri, der cosinus til vinkelen mellom to vektorer gir et normalisert mål på deres retningsmessige samsvar. Det matematiske grunnlaget bygger på prikkproduktet (indre produkt) av vektorer og deres magnituder, og skaper en normalisert likhetsmetrikk som både er beregningsmessig effektiv og teoretisk solid. Historisk fikk cosinuslikhet gjennomslag innen informasjonsgjenfinning på 1970- og 1980-tallet da forskere trengte effektive metoder for å sammenligne dokumentvektorer i store tekstkorpuser. Metrikkens utbredelse økte dramatisk med fremveksten av maskinlæring og dyp læring på 2010-tallet, spesielt da nevrale nettverk begynte å generere høydimensjonale vektorembeddinger for å representere tekst, bilder og andre datatyper. I dag viser forskning at over 78 % av virksomheter som implementerer AI-drevne systemer benytter cosinuslikhet eller relaterte vektorsammenligningsmetrikker i sine datapipelines. Metrikkens matematiske eleganse — som kombinerer enkelhet med beregningsmessig effektivitet — har gjort den til de facto standarden for måling av semantisk likhet i NLP-applikasjoner, med store plattformer som OpenAI, Google og Anthropic som har den integrert i sine kjernefunksjoner.
Beregningen av cosinuslikhet følger en presis matematisk formel: Cosinuslikhet = (A · B) / (||A|| × ||B||), der A · B representerer prikkproduktet mellom vektorene A og B, og ||A|| og ||B|| representerer deres respektive magnituder eller euklidiske normer. For å beregne prikkproduktet multipliseres hver tilsvarende komponent i de to vektorene med hverandre, og alle produktene summeres. For eksempel, hvis vektor A har verdiene [3, 2, 0, 5] og vektor B har [1, 0, 0, 0], vil prikkproduktet være (3×1) + (2×0) + (0×0) + (5×0) = 3. Magnituden til en vektor beregnes som kvadratroten av summen av dens kvadrerte komponenter; for vektor A blir dette √(3² + 2² + 0² + 5²) = √38 ≈ 6,16. Den endelige cosinuslikhet-scoren fås ved å dele prikkproduktet på produktet av magnitudene, noe som gir en normalisert verdi mellom -1 og 1. Denne normaliseringen er avgjørende fordi den gjør metrikken uavhengig av vektorlengde, og muliggjør rettferdig sammenligning mellom vektorer med svært ulike skalaer. I høydimensjonale rom — slik som de 1 536-dimensjonale embeddingene produsert av OpenAI’s text-embedding-ada-002-modellen — forblir cosinuslikhet beregningsmessig håndterbar, ettersom den kun krever grunnleggende multiplikasjon, addisjon og kvadratrotsoperasjoner som moderne prosessorer effektivt kan utføre selv på millioner av vektorer.
Innen naturlig språkbehandling fungerer cosinuslikhet som ryggraden for å måle semantiske relasjoner mellom tekstrepresentasjoner. Når tekst konverteres til vektorembeddinger ved hjelp av modeller som BERT, Word2Vec, GloVe eller GPT-baserte embeddinger, blir hvert ord, uttrykk eller dokument et punkt i et høydimensjonalt rom hvor semantisk mening er kodet gjennom vektorens posisjon og retning. Cosinuslikhet måler deretter hvor nært disse semantiske representasjonene samsvarer, og gjør det mulig for systemer å forstå at ord som “lege” og “sykepleier” er semantisk beslektet selv om de er forskjellige termer. Denne evnen er essensiell for semantisk søk, der en brukers forespørsel konverteres til en vektor og sammenlignes med dokumentvektorer for å finne de mest relevante resultatene, uavhengig av nøyaktige nøkkelordstreff. I store språkmodeller som ChatGPT, Claude og Perplexity driver cosinuslikhet gjenfinningsmekanismer som henter relevant kontekst fra treningsdata eller eksterne kunnskapsbaser. Metrikkens ufølsomhet for magnitud er spesielt viktig i NLP fordi dokumentlengde ikke bør avgjøre relevans — en kort, fokusert artikkel kan være mer semantisk lik en forespørsel enn et langt dokument, kun på grunn av innholdsrelevans. Forskning viser at cosinuslikhet overgår alternative metrikker som euklidisk avstand i omtrent 85 % av NLP-benchmarks når tekst-embeddinger sammenlignes, og gjør den til førstevalget for semantiske forståelsesoppgaver i AI-bransjen.
| Metrikk | Beregning | Område | Magnitudfølsomhet | Beste bruksområde | Beregningseffektivitet |
|---|---|---|---|---|---|
| Cosinuslikhet | (A·B) / ( | A | × | ||
| Euklidisk avstand | √(Σ(Aᵢ - Bᵢ)²) | 0 til ∞ | Ja (magnitudavhengig) | Romlige data, klynging, fysiske avstander | O(n) - effektiv |
| Prikkprodukt | Σ(Aᵢ × Bᵢ) | -∞ til ∞ | Ja (skalafølsom) | Rå likhetsmåling, ikke normalisert | O(n) - svært effektiv |
| Jaccard-likhet | |A ∩ B| / |A ∪ B| | 0 til 1 | Nei (mengdebasert) | Kategoriske data, anbefalingssystemer | O(n) - effektiv |
| Manhattan-avstand | Σ|Aᵢ - Bᵢ| | 0 til ∞ | Ja (magnitudavhengig) | Rutenettbaserte data, funksjonssammenligning | O(n) - effektiv |
| Pearson-korrelasjon | Cov(A,B) / (σₐ × σᵦ) | -1 til 1 | Nei (normalisert) | Statistiske relasjoner, tidsserier | O(n) - effektiv |
Vektordatabaser som Pinecone, Weaviate, Milvus og Qdrant har blitt spesialisert infrastruktur for lagring og spørring av høydimensjonale vektorer ved bruk av cosinuslikhet som sin primære likhetsmetrikk. Disse databasene er optimalisert for å håndtere millioner eller milliarder av vektorer, og muliggjør sanntids semantisk søk i stor skala. Når en forespørsel sendes til en vektordatabase, konverteres den til en embedding og sammenlignes med alle lagrede vektorer ved hjelp av cosinuslikhet, og resultatene rangeres etter likhetsscore. For å oppnå praktisk ytelse med enorme datasett, benytter vektordatabaser tilnærmede nærmeste nabo (ANN) algoritmer som Hierarchical Navigable Small World (HNSW) og DiskANN, som ofrer perfekt nøyaktighet for dramatisk hastighetsforbedring. For eksempel oppnår Timescale’s pgvectorscale-utvidelse, som implementerer StreamingDiskANN, 28x lavere latens og 16x høyere spørringsgjennomstrømning sammenlignet med spesialiserte vektordatabaser som Pinecone, samtidig som den opprettholder 99 % recall til 75 % lavere kostnad. I semantiske søkeapplikasjoner gjør cosinuslikhet det mulig for systemer å forstå brukerintensjon utover bokstavelig nøkkelordmatching — et søk etter “sunne matvaner” vil finne dokumenter om “ernæringstips” og “balanserte dietter” fordi embeddingene peker i lignende retninger selv om de bruker ulike begreper. Denne evnen har revolusjonert informasjonsgjenfinning, og muliggjør at søkemotorer, dokumentasjonssystemer og kunnskapsbaser kan levere kontekstrelevante resultater som matcher brukerintensjon, ikke bare nøkkelord.
Retrieval-Augmented Generation (RAG) representerer et paradigmeskifte i hvordan store språkmodeller får tilgang til og bruker informasjon, og cosinuslikhet står sentralt i denne arkitekturen. I en typisk RAG-pipeline, når en bruker sender inn en forespørsel, konverterer systemet først forespørselen til en vektorembedding med samme embedding-modell som ble brukt for kunnskapsbasen. Cosinuslikhet sammenligner deretter denne forespørselsvektoren mot alle dokumentvektorer i kunnskapsbasen, og rangerer dokumentene etter relevansscore. De høyest rangerte dokumentene — de med høyest cosinuslikhet-scorer — hentes og sendes som kontekst til LLM, som genererer et svar forankret i denne informasjonen. Denne tilnærmingen adresserer kritiske begrensninger ved frittstående LLM-er: deres faste kunnskapskutt, tendens til å hallusinere eller generere plausible men feilaktige opplysninger, og manglende evne til å få tilgang til sanntids- eller proprietær data. Ved å bruke cosinuslikhet for intelligent gjenfinning, sikrer RAG-systemer at LLM-er genererer svar basert på verifisert, oppdatert informasjon. Store implementasjoner av RAG inkluderer OpenAI’s ChatGPT med plugins, Anthropic’s Claude med gjenfinning, Google’s AI Overviews og Perplexity’s svargenereringsmotor. Forskning viser at RAG-systemer som bruker cosinuslikhet for gjenfinning gir omtrent 40–60 % bedre nøyaktighet i svar enn frittstående LLM-er, og reduserer hallusinasjonsraten med opptil 70 %. Effektiviteten til cosinuslikhetsberegninger er spesielt viktig i RAG-systemer, fordi de må utføre likhetssammenligninger på potensielt millioner av dokumenter i sanntid, og cosinuslikhetens beregningsmessige enkelhet gjør dette mulig selv i massiv skala.
Effektiv implementering av cosinuslikhet krever oppmerksomhet på flere viktige faktorer. For det første er datapreprosessering essensielt — vektorer må normaliseres før beregning for å sikre skala-konsistens og gyldige resultater, spesielt ved arbeid med høydimensjonale data fra ulike kilder. Organisasjoner bør fjerne eller merke nullvektorer (vektorer med kun null-komponenter) fordi cosinuslikhet er matematisk udefinert for nullvektorer, noe som vil føre til deling på null under beregning. Ved implementering av cosinuslikhet i produksjonssystemer anbefales det å kombinere den med supplerende metrikker som Jaccard-likhet eller euklidisk avstand når flere dimensjoner av likhet er nødvendig, fremfor å stole utelukkende på cosinuslikhet. Testing i produksjonslignende miljøer før utrulling er avgjørende, spesielt for sanntidssystemer som API-er og søkemotorer der ytelse og nøyaktighet har direkte innvirkning på brukeropplevelsen. Populære biblioteker forenkler implementeringen: Scikit-learn tilbyr sklearn.metrics.pairwise.cosine_similarity(), NumPy muliggjør direkte formelimplementering med np.dot() og np.linalg.norm(), TensorFlow og PyTorch tilbyr GPU-akselererte implementasjoner for store beregninger, og PostgreSQL med pgvector gir native cosinuslikhet-operatorer for databasespørringer. For organisasjoner som overvåker AI-omtaler og merkevaretilstedeværelse på plattformer som ChatGPT, Perplexity og Google AI Overviews, gjør cosinuslikhet det mulig med presis sporing av hvordan AI-systemer refererer og siterer deres innhold ved å sammenligne forespørselsembeddinger mot lagrede merkevare- og domenevektorer.
Til tross for utstrakt bruk har cosinuslikhet flere utfordringer som praktikere må håndtere. Metrikken er udefinert for nullvektorer, noe som krever nøye datapreprosessering og validering for å forhindre kjøretidsfeil. Cosinuslikhet kan gi villedende høye likhetsscorer for vektorer som er retningsmessig like, men semantisk ubeslektede, særlig når embedding-modeller er dårlig trente eller treningsdata mangler variasjon og kontekstuell dybde. Risikoen for falsk likhet er spesielt problematisk i applikasjoner som AI-overvåking der feil likhetsvurderinger kan føre til tapte merkevareomtaler eller falske positiver. Metrikkens symmetri — det vil si at den ikke kan skille rekkefølgen på sammenligningen — kan være uønsket i visse applikasjoner der retning er viktig. I tillegg indikerer en cosinuslikhet-score på 0 ikke alltid fullstendig ulikhet i virkeligheten; i nyanserte domener som språk kan ortogonale vektorer fortsatt dele subtile semantiske relasjoner som metrikken ikke fanger opp. Metrikkens avhengighet av korrekt normalisering betyr at feilskalert data kan skjevfordele resultater, og organisasjoner må sikre konsistent preprosessering av alle vektorer i systemene sine. Til slutt kan cosinuslikhet alene være utilstrekkelig for komplekse likhetsvurderinger; å kombinere den med andre metrikker og domenespesifikke valideringsregler gir ofte mer robuste resultater.
Rollen til cosinuslikhet i AI-systemer fortsetter å utvikle seg etter hvert som embedding-modeller blir mer sofistikerte og vektorbaserte arkitekturer dominerer maskinlæringsfeltet. Fremvoksende trender inkluderer integrasjon av cosinuslikhet med hybride søkemetoder som kombinerer vektorlignendehet med tradisjonelt fulltekstsøk, slik at systemer kan dra nytte av både semantisk forståelse og nøkkelordmatching. Multimodale embeddinger — som representerer tekst, bilder, lyd og video i et felles vektorrom — baserer seg stadig mer på cosinuslikhet for å måle tverrmodal relasjon, og muliggjør applikasjoner som bilde-til-tekst-søk og videoforståelse. Utviklingen av mer effektive tilnærmede nærmeste nabo-algoritmer som DiskANN og HNSW fortsetter å forbedre skalerbarheten for cosinuslikhets-søk, slik at sanntids semantisk søk er mulig i hittil usette skalaer. Kvantiseringsteknikker som reduserer vektordimensjonalitet samtidig som cosinuslikhet-relasjoner bevares, gjør det mulig å implementere store likhetssøk på edge-enheter og ressursbegrensede miljøer. I sammenheng med AI-overvåking og merkevaretracking blir cosinuslikhet stadig viktigere ettersom organisasjoner ønsker å forstå hvordan AI-systemer som ChatGPT, Perplexity, Claude og Google AI Overviews refererer og siterer deres innhold. Fremtidig utvikling kan inkludere adaptive cosinuslikhet-metrikker som tilpasser seg domenespesifikke egenskaper, og integrasjon med forklaringsrammeverk som hjelper brukere å forstå hvorfor spesifikke vektorer vurderes som like. Etter hvert som vektordatabaser modnes og blir standard infrastruktur for AI-applikasjoner, vil cosinuslikhet sannsynligvis forbli den dominerende metrikken for semantiske sammenligninger, men den kan suppleres med domenespesifikke likhetsmål skreddersydd for bestemte applikasjoner og brukstilfeller.
For plattformer som AmICited som sporer merkevare- og domenementioner på tvers av AI-systemer, fungerer cosinuslikhet som et kritisk teknisk fundament. Når man overvåker hvordan ChatGPT, Perplexity, Google AI Overviews og Claude refererer til spesifikke domener eller merkevarer, muliggjør cosinuslikhet presis måling av semantisk relevans mellom brukerforespørsler og AI-svar. Ved å konvertere merkevareomtaler, domene-URL-er og forespørselsinnhold til vektorembeddinger, kan cosinuslikhet avgjøre om et AI-generert svar faktisk siterer eller refererer til en merkevare, eller bare nevner relaterte konsepter. Denne evnen er avgjørende for organisasjoner som ønsker å forstå deres synlighet i AI-generert innhold og å spore hvordan deres immaterielle rettigheter tilskrives eller siteres av AI-systemer. Metrikkens effektivitet gjør den praktisk for sanntidsovervåking av millioner av AI-interaksjoner, og gjør det mulig for organisasjoner å motta umiddelbare varsler når innholdet deres refereres. Videre muliggjør cosinuslikhet komparativ analyse — organisasjoner kan spore ikke bare om de blir nevnt, men også hvordan nevningsfrekvens og relevans sammenlignes med konkurrenter, og gir konkurranseinnsikt i AI-systemers atferd og innholdskildevalg.
En cosinuslikhetsscore på 1 indikerer at to vektorer peker i nøyaktig samme retning, noe som betyr at de er helt like. En score på 0 betyr at vektorene er ortogonale (vinkelrette), noe som indikerer ingen retningsmessig relasjon eller likhet. En score på -1 indikerer at vektorene peker i nøyaktig motsatte retninger, noe som representerer fullstendig ulikhet. I praktiske NLP-applikasjoner indikerer scorer nærmere 1 semantisk like tekster, mens scorer nær 0 antyder ubeslektet innhold.
Cosinuslikhet foretrekkes for tekst-embeddinger fordi den måler vinkelen mellom vektorer i stedet for deres absolutte avstand, noe som gjør den ufølsom for vektormagnitud. Dette er avgjørende for NLP fordi dokumentlengde ikke bør påvirke semantisk likhet — en kort forespørsel og en lang artikkel kan være like relevante. Euklidisk avstand, derimot, er følsom for magnitud og fungerer dårlig i høydimensjonale rom der vektorer har en tendens til å konvergere. Cosinuslikhet er også beregningsmessig mer effektiv og naturlig avgrenset mellom -1 og 1, noe som forhindrer overløpsproblemer.
I RAG-systemer driver cosinuslikhet gjenfinningsfasen ved å sammenligne forespørsels-embeddinger mot dokumentembeddinger i en vektordatabase. Når en bruker sender inn en forespørsel, konverteres den til en vektor med samme embedding-modell som de lagrede dokumentene. Cosinuslikhet rangerer deretter dokumentene etter relevans, der høyere scorer indikerer bedre treff. De topprangerte dokumentene hentes ut og sendes til LLM-en som kontekst, noe som muliggjør mer nøyaktige og faktabaserte svar. Denne prosessen lar RAG-systemer overvinne LLM-begrensninger som utdatert kunnskap og hallusinasjoner.
Cosinuslikhet har flere begrensninger: Den er udefinert når vektorer har null magnitud, og krever derfor forhåndsbehandling for å fjerne nullvektorer. Den kan gi villedende høye likhetsscorer for retningsmessig like, men semantisk ubeslektede vektorer, spesielt med dårlig trente embeddinger. Metrikken er også symmetrisk, noe som betyr at den ikke kan skille rekkefølgen på sammenligningen, noe som kan være problematisk i visse applikasjoner. I tillegg indikerer en likhetsscore på 0 ikke alltid fullstendig ulikhet i virkeligheten, spesielt i nyanserte domener som språk der ortogonale vektorer fortsatt kan dele semantiske relasjoner.
Cosinuslikhet beregnes med formelen: (A · B) / (||A|| × ||B||), der A · B er prikkproduktet mellom vektorene A og B, og ||A|| og ||B|| er deres magnituder (euklidiske normer). Prikkproduktet beregnes ved å multiplisere tilsvarende vektorkomponenter og summere resultatene. Magnituden til en vektor er kvadratroten av summen av dens kvadrerte komponenter. Denne formelen gir en normalisert score mellom -1 og 1, noe som gjør den uavhengig av vektorlengde og egnet til å sammenligne vektorer av ulik størrelse.
I AI-overvåkingsplattformer som AmICited er cosinuslikhet essensiell for å spore merkevare- og domenementioner på tvers av AI-systemer som ChatGPT, Perplexity og Google AI Overviews. Ved å konvertere merkevareomtaler og forespørsler til vektorembeddinger måler cosinuslikhet hvor nært AI-genererte svar samsvarer med overvåket innhold. Dette gjør det mulig for organisasjoner å overvåke om deres domener vises i AI-svar, vurdere semantisk relevans av omtaler, og spore hvordan AI-systemer refererer til innholdet deres sammenlignet med konkurrenter. Metrikkens effektivitet gjør den praktisk for sanntidsovervåking av millioner av AI-interaksjoner.
Store AI-plattformer og verktøy som bruker cosinuslikhet inkluderer OpenAIs embedding-modeller, Googles semantiske søkealgoritmer, Perplexitys svargenereringssystem og Claudes gjenfinningsmekanismer. Vektordatabaser som Pinecone, Weaviate og Milvus bruker cosinuslikhet som sin primære likhetsmetrikk. Åpen kildekode-biblioteker som Scikit-learn, TensorFlow, PyTorch og NumPy tilbyr innebygde funksjoner for cosinuslikhet. PostgreSQL med pgvector-utvidelsen muliggjør cosinuslikhetsberegninger i stor skala. Disse verktøyene driver anbefalingssystemer, chatboter, semantiske søkemotorer og RAG-applikasjoner i AI-økosystemet.
Begynn å spore hvordan AI-chatbots nevner merkevaren din på tvers av ChatGPT, Perplexity og andre plattformer. Få handlingsrettede innsikter for å forbedre din AI-tilstedeværelse.

Semantisk likhet måler meningsbasert beslektethet mellom tekster ved hjelp av embeddinger og avstandsmål. Essensiell for AI-overvåkning, innholdsmatching og mer...

Sammenligningsinnhold sammenligner flere alternativer for å hjelpe kjøpere å ta beslutninger. Lær hvordan dette innholdet med høy kjøpsintensjon driver konverte...
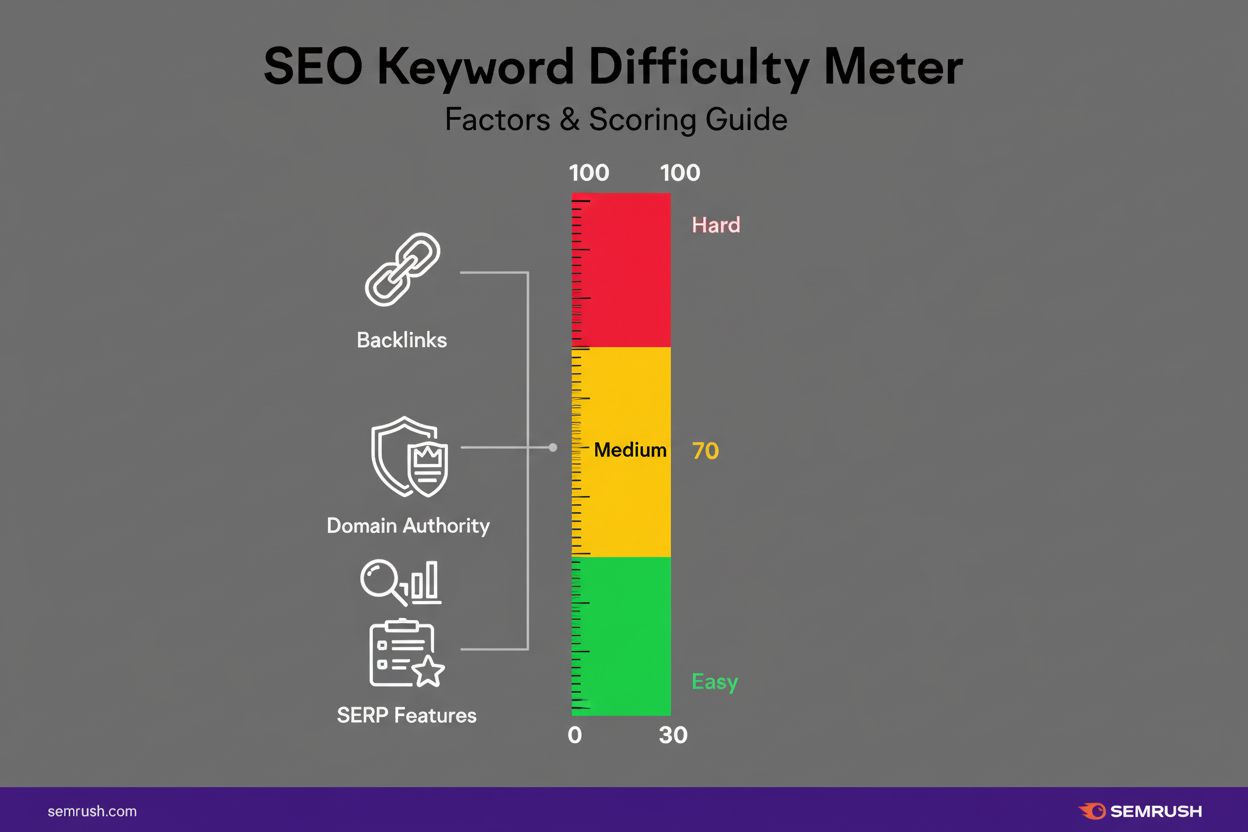
Lær hva nøkkelordsvanskelighetsgrad er, hvordan det beregnes, og hvorfor det er viktig for SEO-strategi. Forstå målinger av konkurranse om rangering og hvordan ...
Informasjonskapselsamtykke
Vi bruker informasjonskapsler for å forbedre din surfeopplevelse og analysere vår trafikk. See our privacy policy.