Podobieństwo semantyczne
Podobieństwo semantyczne mierzy powiązania znaczeniowe między tekstami za pomocą osadzeń i metryk odległości. Niezbędne do monitorowania AI, dopasowania treści ...
11 min czytania
Cosinusowa miara podobieństwa
Cosinusowa miara podobieństwa to matematyczna miara obliczająca podobieństwo pomiędzy dwoma niezerowymi wektorami poprzez wyznaczenie kosinusa kąta między nimi; wynik mieści się w zakresie od -1 do 1. Jest szeroko wykorzystywana w uczeniu maszynowym, przetwarzaniu języka naturalnego i systemach AI do pomiaru semantycznego podobieństwa między osadzeniami tekstów i reprezentacjami wektorowymi, niezależnie od długości wektora.
Definicja cosinusowej miary podobieństwa
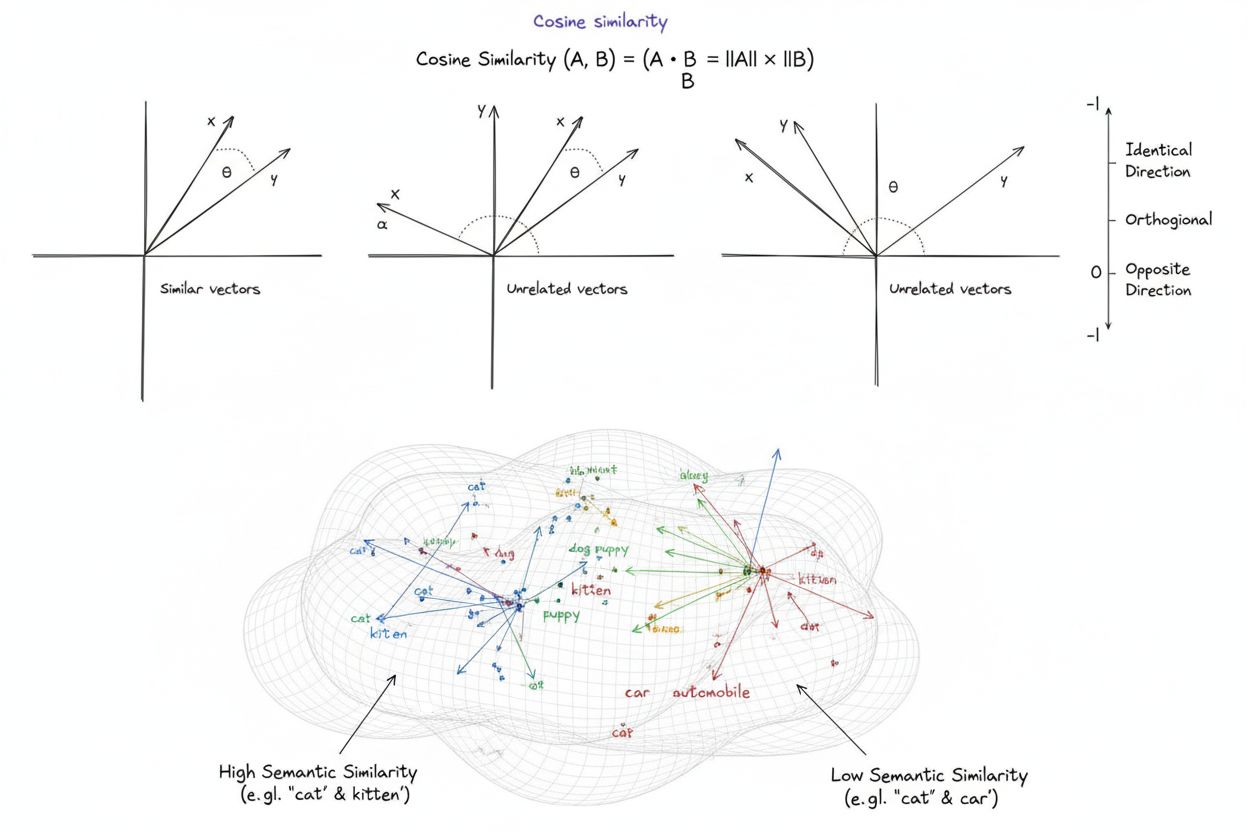
Cosinusowa miara podobieństwa to matematyczna miara określająca podobieństwo pomiędzy dwoma niezerowymi wektorami poprzez wyznaczenie kosinusa kąta między nimi w przestrzeni wielowymiarowej. Metryka ta przyjmuje wartości od -1 do 1, gdzie 1 oznacza, że wektory są skierowane w identycznym kierunku, 0 wskazuje na wektory ortogonalne (prostopadłe) bez relacji kierunkowej, a -1 oznacza wektory skierowane dokładnie przeciwnie. W praktyce cosinusowa miara podobieństwa jest szczególnie cenna, ponieważ mierzy zbieżność kierunkową, a nie bezwzględną odległość, przez co jest niewrażliwa na długość wektora. Właściwość ta sprawia, że jest wyjątkowo przydatna do porównywania osadzeń tekstowych, wektorów dokumentów oraz reprezentacji semantycznych, gdzie długość lub skala danych nie powinna wpływać na ocenę podobieństwa. Metryka ta stała się fundamentem współczesnej sztucznej inteligencji, przetwarzania języka naturalnego oraz systemów uczenia maszynowego, napędzając wszystko — od wyszukiwarek po algorytmy rekomendacyjne i zastosowania dużych modeli językowych.
Kontekst historyczny i podstawa matematyczna
Koncepcja cosinusowej miary podobieństwa wywodzi się z podstaw algebry liniowej i trygonometrii, gdzie kosinus kąta między dwoma wektorami dostarcza znormalizowanej miary ich zbieżności kierunkowej. Podstawa matematyczna opiera się na iloczynie skalarnym (iloczynie wewnętrznym) wektorów oraz ich długościach, tworząc znormalizowaną metrykę podobieństwa, która jest zarówno wydajna obliczeniowo, jak i teoretycznie uzasadniona. Historycznie cosinusowa miara podobieństwa zyskała popularność w wyszukiwaniu informacji w latach 70. i 80., gdy badacze potrzebowali wydajnych metod porównywania wektorów dokumentów w dużych zbiorach tekstowych. Znacząco przyspieszyła jej adopcja wraz z rozwojem uczenia maszynowego i uczenia głębokiego w latach 2010., szczególnie gdy sieci neuronowe zaczęły generować wysoko wymiarowe osadzenia wektorowe dla tekstów, obrazów i innych typów danych. Obecnie badania wskazują, że ponad 78% przedsiębiorstw wdrażających systemy oparte na AI wykorzystuje cosinusową miarę podobieństwa lub pokrewne metryki porównywania wektorów w swoich pipeline’ach danych. Elegancja tej metryki — łącząca prostotę z wydajnością obliczeniową — sprawiła, że stała się ona standardem w pomiarze semantycznego podobieństwa w zastosowaniach NLP, a największe platformy, takie jak OpenAI, Google czy Anthropic, włączyły ją do swoich kluczowych rozwiązań.
Wyjaśnienie techniczne: Jak działa cosinusowa miara podobieństwa
Obliczenie cosinusowej miary podobieństwa opiera się na precyzyjnym wzorze matematycznym: Cosine Similarity = (A · B) / (||A|| × ||B||), gdzie A · B oznacza iloczyn skalarny wektorów A i B, a ||A|| oraz ||B|| to odpowiednio ich długości (normy euklidesowe). Aby wyznaczyć iloczyn skalarny, należy pomnożyć odpowiadające sobie składniki obu wektorów i zsumować wyniki. Przykładowo, dla wektora A o wartościach [3, 2, 0, 5] i wektora B o wartościach [1, 0, 0, 0], iloczyn skalarny wynosi (3×1) + (2×0) + (0×0) + (5×0) = 3. Długość wektora oblicza się jako pierwiastek kwadratowy z sumy kwadratów jego składników; dla A będzie to √(3² + 2² + 0² + 5²) = √38 ≈ 6,16. Końcowy wynik cosinusowej miary podobieństwa uzyskujemy, dzieląc iloczyn skalarny przez iloczyn długości wektorów, co daje znormalizowaną wartość z zakresu od -1 do 1. Normalizacja ta jest kluczowa, ponieważ czyni metrykę niezależną od długości wektorów, umożliwiając obiektywne porównanie wektorów o bardzo różnej skali. W przestrzeniach o bardzo wielu wymiarach — jak w przypadku osadzeń o 1 536 wymiarach generowanych przez model OpenAI text-embedding-ada-002 — cosinusowa miara podobieństwa pozostaje obliczeniowo efektywna, wymagając jedynie podstawowych operacji mnożenia, dodawania i pierwiastkowania, które nowoczesne procesory wykonują wydajnie nawet dla milionów wektorów.
Cosinusowa miara podobieństwa w NLP i systemach AI
W przetwarzaniu języka naturalnego cosinusowa miara podobieństwa stanowi fundament pomiaru relacji semantycznych pomiędzy reprezentacjami tekstów. Po zamianie tekstu na osadzenia wektorowe za pomocą modeli takich jak BERT, Word2Vec, GloVe czy osadzenia oparte na GPT, każde słowo, fraza czy dokument staje się punktem w wielowymiarowej przestrzeni, gdzie znaczenie semantyczne zakodowane jest przez pozycję i kierunek wektora. Cosinusowa miara podobieństwa mierzy wtedy, jak bardzo te reprezentacje są do siebie zbliżone kierunkowo, co pozwala systemom rozumieć, że słowa „lekarz” i „pielęgniarka” są semantycznie powiązane, mimo że się różnią. Ta właściwość jest niezbędna w wyszukiwaniu semantycznym, gdzie zapytanie użytkownika jest zamieniane na wektor i porównywane z wektorami dokumentów, aby znaleźć najbardziej istotne wyniki — niezależnie od dokładnych dopasowań słów kluczowych. W dużych modelach językowych jak ChatGPT, Claude czy Perplexity, cosinusowa miara podobieństwa napędza mechanizmy wyszukiwania kontekstu z danych treningowych lub zewnętrznych baz wiedzy. Niewrażliwość metryki na długość jest szczególnie ważna w NLP, ponieważ długość dokumentu nie powinna decydować o trafności — krótki, zwięzły artykuł może być semantycznie bliższy zapytaniu niż długi tekst, jeśli tylko jego treść jest bardziej adekwatna. Badania wskazują, że cosinusowa miara podobieństwa przewyższa alternatywne metryki, takie jak odległość euklidesowa, w około 85% benchmarków NLP przy porównywaniu osadzeń tekstowych, przez co jest preferowanym wyborem w zadaniach rozumienia semantycznego w branży AI.
Tabela porównawcza: Cosinusowa miara podobieństwa a pokrewne metryki
| Metryka | Sposób obliczania | Zakres | Wrażliwość na długość | Najlepsze zastosowanie | Złożoność obliczeniowa |
|---|---|---|---|---|---|
| Cosinusowa miara podobieństwa | (A·B) / ( | A | × | ||
| Odległość euklidesowa | √(Σ(Aᵢ - Bᵢ)²) | 0 do ∞ | Tak (zależna od długości) | Dane przestrzenne, klasteryzacja, odległości fizyczne | O(n) - wydajna |
| Iloczyn skalarny | Σ(Aᵢ × Bᵢ) | -∞ do ∞ | Tak (wrażliwy na skalę) | Surowy pomiar podobieństwa, brak normalizacji | O(n) - bardzo wydajna |
| Podobieństwo Jaccarda | |A ∩ B| / |A ∪ B| | 0 do 1 | Nie (zbiorowe) | Dane kategoryczne, systemy rekomendacji | O(n) - wydajna |
| Odległość Manhattan | Σ|Aᵢ - Bᵢ| | 0 do ∞ | Tak (zależna od długości) | Dane siatkowe, porównywanie cech | O(n) - wydajna |
| Korelacja Pearsona | Cov(A,B) / (σₐ × σᵦ) | -1 do 1 | Nie (znormalizowana) | Zależności statystyczne, szeregi czasowe | O(n) - wydajna |
Szczegóły: Cosinusowa miara podobieństwa w bazach wektorowych i wyszukiwaniu semantycznym
Bazy wektorowe takie jak Pinecone, Weaviate, Milvus i Qdrant to wyspecjalizowana infrastruktura do przechowywania i wyszukiwania wysoko wymiarowych wektorów z wykorzystaniem cosinusowej miary podobieństwa jako głównej metryki. Bazy te zoptymalizowane są do obsługi milionów, a nawet miliardów wektorów, pozwalając na wyszukiwanie semantyczne w czasie rzeczywistym w dużej skali. Gdy zapytanie trafia do bazy wektorowej, jest zamieniane na embedding i porównywane z wszystkimi zapisanymi wektorami przy użyciu cosinusowej miary podobieństwa, a wyniki są sortowane według uzyskanego wyniku podobieństwa. Aby uzyskać wydajność przy bardzo dużych zbiorach danych, bazy wektorowe wykorzystują przybliżone algorytmy najbliższych sąsiadów (ANN) takie jak Hierarchical Navigable Small World (HNSW) i DiskANN, które poświęcają dokładność na rzecz ogromnego przyspieszenia wyszukiwania. Przykładowo, rozszerzenie pgvectorscale dla Timescale, implementujące StreamingDiskANN, osiąga 28 razy niższe opóźnienia i 16 razy większą przepustowość zapytań w porównaniu do wyspecjalizowanych baz wektorowych takich jak Pinecone, zachowując 99% recall przy 75% niższych kosztach. W aplikacjach wyszukiwania semantycznego cosinusowa miara podobieństwa pozwala systemom rozumieć intencję użytkownika poza dosłownym dopasowaniem słów kluczowych — wyszukiwanie „zdrowe nawyki żywieniowe” zwróci dokumenty o „poradach żywieniowych” czy „zbilansowanej diecie”, bo ich embeddingi skierowane są w podobnych kierunkach, mimo różnic w słownictwie. Zdolność ta zrewolucjonizowała wyszukiwanie informacji, pozwalając wyszukiwarkom i bazom wiedzy dostarczać wyniki dopasowane do intencji użytkownika, nie tylko do słów kluczowych.
Cosinusowa miara podobieństwa w Retrieval-Augmented Generation (RAG) i zastosowaniach LLM
Retrieval-Augmented Generation (RAG) to nowy paradygmat dostępu i wykorzystywania informacji przez duże modele językowe, którego podstawą jest cosinusowa miara podobieństwa. W typowym pipeline RAG zapytanie użytkownika zostaje najpierw zamienione na osadzenie wektorowe przy pomocy tego samego modelu embeddingowego, którym wektoryzowano bazę wiedzy. Następnie cosinusowa miara podobieństwa porównuje ten wektor zapytania z wektorami dokumentów w bazie, tworząc ranking według trafności. Najwyżej ocenione dokumenty — te o najwyższych wynikach cosinusowej miary podobieństwa — są pobierane i przekazywane jako kontekst do LLM, który generuje odpowiedź opartą na tych informacjach. Podejście to rozwiązuje kluczowe ograniczenia samodzielnych LLM: ograniczoną aktualność wiedzy, tendencję do halucynacji oraz brak dostępu do informacji w czasie rzeczywistym czy do danych zastrzeżonych. Dzięki wykorzystaniu cosinusowej miary podobieństwa do inteligentnego wyszukiwania systemy RAG zapewniają, że odpowiedzi LLM są oparte na zweryfikowanych i aktualnych informacjach. Najważniejsze implementacje RAG to ChatGPT z pluginami od OpenAI, Claude z retrieval od Anthropic, Google AI Overviews oraz silnik generowania odpowiedzi Perplexity. Badania pokazują, że systemy RAG wykorzystujące cosinusową miarę podobieństwa poprawiają trafność odpowiedzi o około 40-60% względem samych LLM, a wskaźnik halucynacji spada nawet o 70%. Wydajność obliczeń cosinusowej miary podobieństwa jest szczególnie ważna w systemach RAG, ponieważ muszą one porównywać podobieństwo z potencjalnie milionami dokumentów w czasie rzeczywistym, a prostota obliczeniowa tej metryki czyni to możliwym nawet w ogromnej skali.
Wdrożenie w praktyce i dobre praktyki
Efektywne wdrożenie cosinusowej miary podobieństwa wymaga uwzględnienia kilku kluczowych aspektów. Po pierwsze, niezbędne jest wstępne przetwarzanie danych — wektory powinny być normalizowane przed obliczeniem podobieństwa, aby zachować spójność skali i poprawność wyników, szczególnie w przypadku wejść o wysokiej liczbie wymiarów z różnych źródeł. Organizacje powinny usuwać lub oznaczać wektory zerowe (wszystkie składniki równe zero), ponieważ cosinusowa miara podobieństwa jest dla nich matematycznie niezdefiniowana i może powodować błędy dzielenia przez zero. W systemach produkcyjnych warto łączyć cosinusową miarę podobieństwa z innymi metrykami, np. Jaccarda czy odległością euklidesową, gdy potrzebna jest wielowymiarowa ocena podobieństwa, zamiast polegać wyłącznie na jednej metryce. Testowanie w środowiskach zbliżonych do produkcyjnych przed wdrożeniem jest kluczowe, zwłaszcza dla systemów czasu rzeczywistego, takich jak API i wyszukiwarki, gdzie wydajność i precyzja bezpośrednio wpływają na doświadczenie użytkownika. Popularne biblioteki upraszczają implementację: Scikit-learn udostępnia sklearn.metrics.pairwise.cosine_similarity(), NumPy pozwala na implementację wzoru za pomocą np.dot() i np.linalg.norm(), TensorFlow i PyTorch oferują wersje przyspieszane przez GPU dla dużych zbiorów danych, a PostgreSQL z pgvector zapewnia natywną obsługę miary cosinusowej na poziomie bazy danych. Dla organizacji monitorujących wzmianki AI i obecność marki na platformach takich jak ChatGPT, Perplexity czy Google AI Overviews, cosinusowa miara podobieństwa umożliwia precyzyjne śledzenie sposobu, w jaki systemy AI odnoszą się do ich treści przez porównywanie embeddingów zapytań ze zbiorem wektorów marek i domen.
Kluczowe aspekty i zalety cosinusowej miary podobieństwa
- Niezależność od długości: Mierzy zbieżność kierunkową, nie odległość, przez co idealnie nadaje się do porównywania wektorów o różnej długości i skali
- Wydajność w wysokich wymiarach: Sprawdza się w przestrzeniach o dużej liczbie wymiarów (100+), gdzie tradycyjne metryki odległości tracą skuteczność lub stają się niepraktyczne obliczeniowo
- Prostota obliczeniowa: Wymaga jedynie prostych operacji (mnożenie, dodawanie, pierwiastek), co umożliwia sprawną implementację w różnych językach i na wielu platformach
- Ograniczony zakres wyników: Zwraca znormalizowane wartości w przedziale od -1 do 1, co zapobiega problemom z przepełnieniem i pozwala intuicyjnie interpretować poziom podobieństwa
- Semantyczna zgodność: Naturalnie wychwytuje relacje semantyczne w embeddingach tekstowych, co czyni ją idealną do zadań NLP i rozumienia języka
- Skalowalność: Umożliwia wydajną obsługę wsadową i optymalizację dla rzadkich wektorów z wieloma zerami
- Standard branżowy: Szeroko stosowana w platformach AI, bazach wektorowych i frameworkach uczenia maszynowego, zapewniając kompatybilność i interoperacyjność
- Wydajność w czasie rzeczywistym: Pozwala na szybkie wyszukiwanie podobieństwa nawet wśród milionów wektorów, wspierając aplikacje czasu rzeczywistego, takie jak wyszukiwarki i systemy rekomendacji
Wyzwania i ograniczenia zastosowań cosinusowej miary podobieństwa
Pomimo powszechnego zastosowania cosinusowa miara podobieństwa niesie ze sobą wyzwania, którym należy stawić czoła. Metryka ta jest niezdefiniowana dla wektorów zerowych, co wymaga starannego wstępnego przetwarzania i walidacji danych, aby uniknąć błędów wykonania. Cosinusowa miara podobieństwa może generować myląco wysokie wyniki podobieństwa dla wektorów skierowanych w tym samym kierunku, lecz semantycznie niepowiązanych, szczególnie gdy modele embeddingów są słabo wytrenowane lub dane treningowe nie zawierają wystarczającej różnorodności i kontekstu. Ryzyko fałszywego podobieństwa jest szczególnie istotne w aplikacjach takich jak monitoring AI, gdzie błędna ocena podobieństwa może prowadzić do pominięcia wzmianek o marce lub fałszywych alarmów. Symetryczność metryki — brak rozróżnienia kierunku porównania — może być niepożądana w zastosowaniach, gdzie kierunek ma znaczenie. Ponadto wynik cosinusowej miary podobieństwa równy 0 nie zawsze oznacza całkowity brak podobieństwa w praktyce; w języku ortogonalne wektory mogą wiązać się z subtelnymi relacjami semantycznymi, których metryka nie wychwytuje. Uzależnienie od poprawnej normalizacji powoduje, że niespójnie skalowane dane mogą zniekształcać wyniki, dlatego organizacje muszą zapewnić jednolite przetwarzanie wszystkich wektorów. Ostatecznie cosinusowa miara podobieństwa często nie wystarcza do złożonych ocen podobieństwa — połączenie jej z innymi metrykami i regułami branżowymi daje zwykle bardziej rzetelne wyniki.
Trendy i przyszłość cosinusowej miary podobieństwa w AI
Rola cosinusowej miary podobieństwa w systemach AI stale ewoluuje wraz z rozwojem modeli embeddingowych i dominacją architektur wektorowych w uczeniu maszynowym. Wśród trendów wyróżnia się integracja cosinusowej miary podobieństwa z wyszukiwaniem hybrydowym, łączącym podobieństwo wektorowe z tradycyjnym wyszukiwaniem tekstowym, co pozwala systemom wykorzystywać zarówno rozumienie semantyczne, jak i dopasowanie słów kluczowych. Osadzenia multimodalne — reprezentujące tekst, obrazy, dźwięk i wideo w jednej przestrzeni wektorowej — coraz częściej polegają na cosinusowej miarze podobieństwa do pomiaru zależności między różnymi modalnościami, umożliwiając np. wyszukiwanie obraz-tekst czy zrozumienie wideo. Rozwój efektywniejszych algorytmów approximate nearest neighbor (jak DiskANN czy HNSW) wciąż poprawia skalowalność wyszukiwań opartych na cosinusowej miarze podobieństwa, czyniąc semantyczne wyszukiwanie w czasie rzeczywistym możliwym na niespotykaną dotąd skalę. Techniki kwantyzacji pozwalające zmniejszyć wymiarowość wektorów przy zachowaniu relacji cosinusowej miary podobieństwa umożliwiają wdrażanie dużych wyszukiwarek podobieństwa na urządzeniach brzegowych i w środowiskach o ograniczonych zasobach. W kontekście monitoringu AI i śledzenia marek cosinusowa miara podobieństwa zyskuje na znaczeniu, gdy organizacje chcą wiedzieć, jak systemy takie jak ChatGPT, Perplexity, Claude czy Google AI Overviews cytują i referują ich treści. Przyszłość może przynieść adaptacyjne metryki cosinusowe, dostosowujące się do specyfiki danej domeny, oraz integrację z frameworkami wyjaśnialności, pomagającymi zrozumieć, dlaczego dane wektory uznane są za podobne. Wraz z dojrzewaniem baz wektorowych do roli standardowej infrastruktury AI cosinusowa miara podobieństwa prawdopodobnie pozostanie dominującą metryką porównania semantycznego, choć może być uzupełniana przez specyficzne dla domen metryki podobieństwa.
Cosinusowa miara podobieństwa a monitoring cytowań AI
Dla platform takich jak AmICited, które śledzą wzmianki o markach i domenach w systemach AI, cosinusowa miara podobieństwa stanowi kluczową podstawę techniczną. Monitorując, jak ChatGPT, Perplexity, Google AI Overviews i Claude odnoszą się do konkretnych domen czy marek, cosinusowa miara podobieństwa umożliwia precyzyjny pomiar semantycznej zgodności pomiędzy zapytaniami użytkowników a odpowiedziami AI. Dzięki zamianie wzmianek o marce, adresów domen i treści zapytań na embeddingi, cosinusowa miara podobieństwa pozwala określić, czy odpowiedź AI rzeczywiście cytuje lub odnosi się do marki, a nie tylko wspomina powiązane pojęcia. Ta możliwość jest kluczowa dla organizacji chcących zrozumieć swoją widoczność w treściach generowanych przez AI i śledzić, jak ich własność intelektualna jest przypisywana i cytowana przez systemy AI. Wydajność tej metryki umożliwia monitoring milionów interakcji AI w czasie rzeczywistym, pozwalając organizacjom na natychmiastowe powiadomienia o odniesieniach do ich treści. Ponadto cosinusowa miara podobieństwa umożliwia analizę porównawczą — organizacje mogą śledzić nie tylko, czy są wspominane, ale także jak często i jak bardzo są istotne w porównaniu z konkurencją, uzyskując w ten sposób cenną wiedzę o zachowaniach systemów AI i źródłach ich treści.
