
Semantisk Likhet
Semantisk likhet mäter meningsbaserad närhet mellan texter med hjälp av inbäddningar och avståndsmått. Avgörande för AI-övervakning, innehållsmatchning och varu...
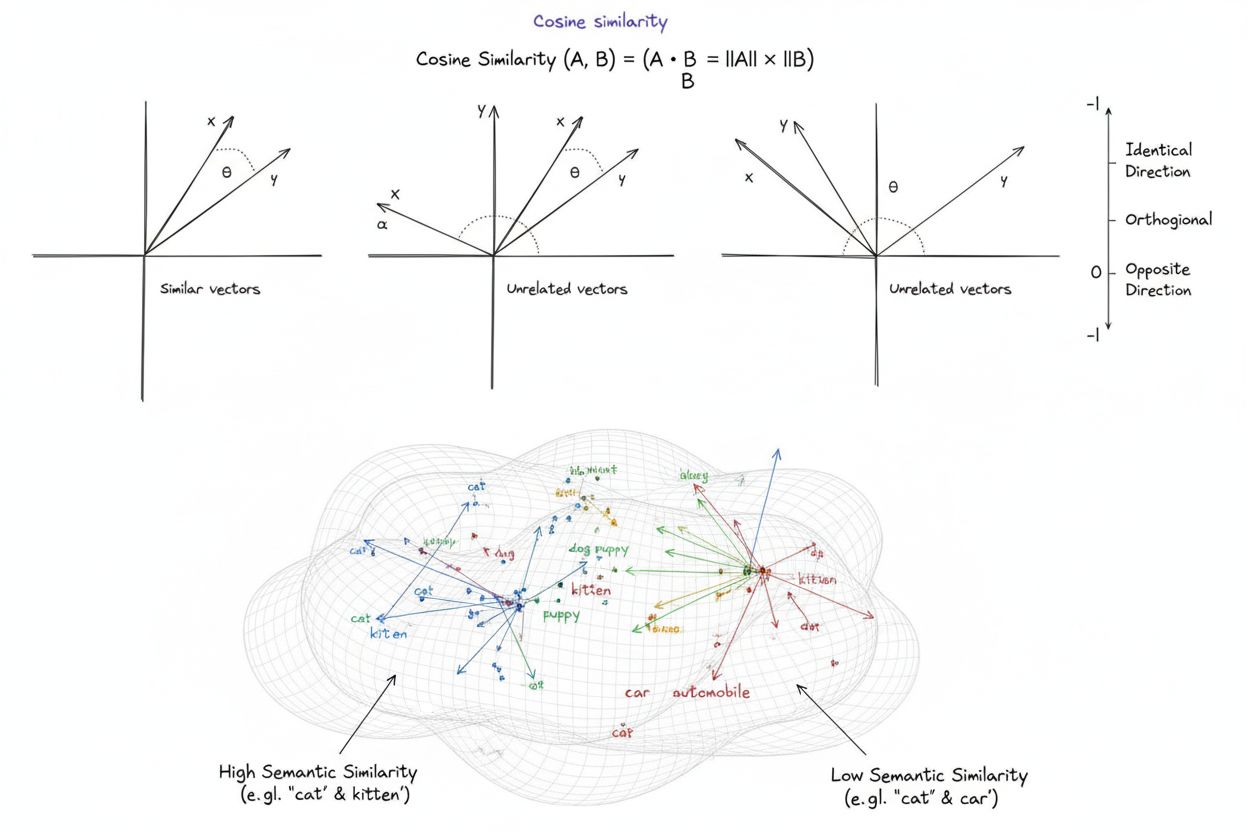
Cosinuslikhet är ett matematiskt mått som beräknar likheten mellan två icke-nollvektorer genom att bestämma cosinus av vinkeln mellan dem, vilket ger ett värde från -1 till 1. Det används ofta inom maskininlärning, naturlig språkbehandling och AI-system för att mäta semantisk likhet mellan textinbäddningar och vektorrepresentationer, oavsett vektorns storlek.
Cosinuslikhet är ett matematiskt mått som beräknar likheten mellan två icke-nollvektorer genom att bestämma cosinus av vinkeln mellan dem, vilket ger ett värde från -1 till 1. Det används ofta inom maskininlärning, naturlig språkbehandling och AI-system för att mäta semantisk likhet mellan textinbäddningar och vektorrepresentationer, oavsett vektorns storlek.
Cosinuslikhet är ett matematiskt mått som beräknar likheten mellan två icke-nollvektorer genom att bestämma cosinus för vinkeln mellan dem i ett flerdimensionellt rum. Måttet ger ett värde från -1 till 1, där ett värde på 1 indikerar vektorer som pekar i identiska riktningar, 0 indikerar ortogonala (vinkelräta) vektorer utan någon riktad relation, och -1 indikerar vektorer som pekar i exakt motsatta riktningar. I praktiska tillämpningar är cosinuslikhet särskilt värdefull eftersom den mäter riktad inriktning snarare än absolut avstånd, vilket gör den oberoende av vektorns storlek. Denna egenskap gör den exceptionellt användbar för att jämföra textinbäddningar, dokumentvektorer och semantiska representationer där längden eller skalan på data inte bör påverka likhetsbedömningar. Måttet har blivit grundläggande för modern artificiell intelligens, naturlig språkbehandling och maskininlärning, och driver allt från sökmotorer till rekommendationsalgoritmer till applikationer för stora språkmodeller.
Konceptet cosinuslikhet uppstod från grundläggande linjär algebra och trigonometri, där cosinus för vinkeln mellan två vektorer ger ett normaliserat mått på deras inriktning. Den matematiska grunden bygger på skalärprodukt (inre produkt) av vektorer och deras storlekar, vilket skapar ett normaliserat likhetsmått som är både beräkningsmässigt effektivt och teoretiskt korrekt. Historiskt fick cosinuslikhet genomslag inom informationsåtervinning under 1970- och 1980-talet när forskare behövde effektiva metoder för att jämföra dokumentvektorer i stora textkorpusar. Måttets användning accelererade dramatiskt med framväxten av maskininlärning och djupinlärning under 2010-talet, särskilt när neurala nätverk började skapa högdimensionella vektorinbäddningar för att representera text, bilder och andra datatyper. Idag visar forskning att över 78 % av företag som implementerar AI-drivna system använder cosinuslikhet eller relaterade vektorjämförelsemått i sina datapipelines. Måttets matematiska elegans—kombinerad enkelhet med beräkningsmässig effektivitet—har gjort det till de facto-standard för att mäta semantisk likhet i NLP-applikationer, där stora plattformar som OpenAI, Google och Anthropic har införlivat det i sina kärnsystem.
Beräkningen av cosinuslikhet följer en exakt matematisk formel: Cosinuslikhet = (A · B) / (||A|| × ||B||), där A · B representerar skalärprodukten av vektorerna A och B, och ||A|| samt ||B|| representerar deras respektive storlekar eller euklidiska normer. För att beräkna skalärprodukten multipliceras varje motsvarande komponent av de två vektorerna och alla produkter summeras. Om till exempel vektor A innehåller värdena [3, 2, 0, 5] och vektor B innehåller [1, 0, 0, 0], blir skalärprodukten (3×1) + (2×0) + (0×0) + (5×0) = 3. Storleken på en vektor beräknas som kvadratroten av summan av dess kvadrerade komponenter; för vektor A skulle detta vara √(3² + 2² + 0² + 5²) = √38 ≈ 6,16. Det slutliga cosinuslikhet-värdet erhålls genom att dividera skalärprodukten med produkten av storlekarna, vilket ger ett normaliserat värde mellan -1 och 1. Denna normalisering är avgörande eftersom den gör måttet oberoende av vektorns längd, vilket möjliggör rättvis jämförelse mellan vektorer av mycket olika skala. I högdimensionella rum—som de 1 536-dimensionella inbäddningar som produceras av OpenAI:s text-embedding-ada-002-modell—förblir cosinuslikhet beräkningsmässigt hanterbar och kräver endast grundläggande multiplikations-, additions- och kvadratrotsoperationer som moderna processorer effektivt kan utföra även över miljontals vektorer.
Inom naturlig språkbehandling fungerar cosinuslikhet som ryggraden för att mäta semantiska relationer mellan textrepresentationer. När text konverteras till vektorinbäddningar med modeller som BERT, Word2Vec, GloVe eller GPT-baserade inbäddningar blir varje ord, fras eller dokument en punkt i ett högdimensionellt rum där semantisk betydelse kodas genom vektorns position och riktning. Cosinuslikhet mäter sedan hur nära dessa semantiska representationer ligger, vilket gör det möjligt för system att förstå att ord som “läkare” och “sjuksköterska” är semantiskt relaterade trots att de är olika termer. Denna förmåga är avgörande för semantisk sökning, där en användares fråga omvandlas till en vektor och jämförs med dokumentvektorer för att hitta de mest relevanta resultaten, oavsett exakta nyckelordsmatchningar. I stora språkmodeller som ChatGPT, Claude och Perplexity driver cosinuslikhet de hämtmekanismer som hämtar relevant kontext från träningsdata eller externa kunskapsbaser. Måttets okänslighet för storlek är särskilt viktigt i NLP eftersom dokumentlängd inte bör avgöra relevans—en kort, fokuserad artikel kan vara mer semantiskt lik en fråga än ett långt dokument på grund av innehållets relevans. Forskning visar att cosinuslikhet överträffar alternativa mått som euklidiskt avstånd i cirka 85 % av NLP-benchmarks vid jämförelse av textinbäddningar, vilket gör det till det föredragna valet för semantiska förståelseuppgifter inom AI-industrin.
| Mått | Beräkningsmetod | Intervall | Känslighet för storlek | Bästa användningsområde | Beräkningskomplexitet |
|---|---|---|---|---|---|
| Cosinuslikhet | (A·B) / ( | A | × | ||
| Euklidiskt avstånd | √(Σ(Aᵢ - Bᵢ)²) | 0 till ∞ | Ja (beroende av storlek) | Rumsliga data, klustring, fysiska avstånd | O(n) - effektiv |
| Skalärprodukt | Σ(Aᵢ × Bᵢ) | -∞ till ∞ | Ja (känslig för skala) | Rå likhetsmätning, ej normaliserad | O(n) - mycket effektiv |
| Jaccardlikhet | |A ∩ B| / |A ∪ B| | 0 till 1 | Nej (mängdbaserad) | Kategoriska data, rekommendationssystem | O(n) - effektiv |
| Manhattan-avstånd | Σ|Aᵢ - Bᵢ| | 0 till ∞ | Ja (beroende av storlek) | Rutnätsbaserade data, funktionsjämförelse | O(n) - effektiv |
| Pearsons korrelation | Cov(A,B) / (σₐ × σᵦ) | -1 till 1 | Nej (normaliserad) | Statistiska relationer, tidsserier | O(n) - effektiv |
Vektordatabaser som Pinecone, Weaviate, Milvus och Qdrant har vuxit fram som specialiserad infrastruktur för att lagra och fråga på högdimensionella vektorer med cosinuslikhet som sitt primära likhetsmått. Dessa databaser är optimerade för att hantera miljontals eller miljarder vektorer, vilket möjliggör semantisk sökning i realtid i stor skala. När en fråga skickas till en vektordatabas konverteras den till en inbäddning och jämförs med alla lagrade vektorer med cosinuslikhet, och resultaten rankas efter likhetspoäng. För att uppnå praktisk prestanda med massiva datamängder använder vektordatabaser approximativa närmaste granne (ANN)-algoritmer såsom Hierarchical Navigable Small World (HNSW) och DiskANN, som offrar perfekt noggrannhet för dramatiskt ökad hastighet. Till exempel uppnår Timescales pgvectorscale-tillägg, som implementerar StreamingDiskANN, 28x lägre latens och 16x högre frågekapacitet jämfört med specialiserade vektordatabaser som Pinecone, samtidigt som den bibehåller 99 % recall till 75 % lägre kostnad. I semantiska sökapplikationer gör cosinuslikhet det möjligt för system att förstå användarens intentioner bortom bokstavlig nyckelordsmatchning—en sökning på “hälsosamma matvanor” hämtar dokument om “näringstips” och “balanserade dieter” eftersom deras inbäddningar pekar i liknande riktningar trots att olika terminologi används. Denna förmåga har revolutionerat informationssökning och möjliggjort för sökmotorer, dokumentationssystem och kunskapsbaser att leverera kontextuellt relevanta resultat som matchar användarens intention snarare än bara nyckelord.
Retrieval-Augmented Generation (RAG) representerar ett paradigmskifte i hur stora språkmodeller får tillgång till och använder information, och cosinuslikhet är central för denna arkitektur. I en typisk RAG-pipeline, när en användare skickar in en fråga, konverterar systemet frågan till en vektorinbäddning med samma inbäddningsmodell som användes för att vektorisera kunskapsbasen. Cosinuslikhet jämför sedan denna frågevektor med alla dokumentvektorer i kunskapsbasen och rankar dokumenten efter relevanspoäng. De högst rankade dokumenten—de med högst cosinuslikhet—hämtas och skickas som kontext till LLM:en, som genererar ett svar baserat på den hämtade informationen. Detta tillvägagångssätt adresserar kritiska begränsningar hos fristående LLM:er: deras fasta kunskapsgränser, tendens att hallucinera eller generera trovärdiga men felaktiga uppgifter, och oförmåga att få tillgång till realtids- eller proprietär information. Genom att använda cosinuslikhet för intelligent hämtning säkerställer RAG-system att LLM:er genererar svar baserade på verifierad, uppdaterad information. Stora implementationer av RAG inkluderar OpenAI:s ChatGPT med plugins, Anthropics Claude med hämtning, Googles AI Overviews och Perplexitys svarsgenereringsmotor. Forskning visar att RAG-system som använder cosinuslikhet för hämtning förbättrar svarens noggrannhet med cirka 40-60 % jämfört med fristående LLM:er, samtidigt som hallucinationsfrekvensen minskar med upp till 70 %. Effektiviteten hos cosinuslikhetsberäkningar är särskilt viktig i RAG-system eftersom de måste utföra likhetsjämförelser över potentiellt miljontals dokument i realtid, och cosinuslikhetens beräkningsenkelhet gör detta möjligt även i mycket stor skala.
Effektiv implementering av cosinuslikhet kräver uppmärksamhet på flera viktiga faktorer. För det första är datapreprocessing avgörande—vektorer måste normaliseras före beräkning för att säkerställa enhetlig skala och giltiga resultat, särskilt vid arbete med högdimensionella indata från olika källor. Organisationer bör ta bort eller flagga nollvektorer (vektorer med alla komponenter noll) eftersom cosinuslikhet är matematiskt odefinierad för sådana vektorer, vilket skulle orsaka division-med-noll-fel vid beräkning. Vid implementering av cosinuslikhet i produktionssystem rekommenderas att kombinera det med kompletterande mått som Jaccardlikhet eller euklidiskt avstånd när flera dimensioner av likhet behövs, snarare än att enbart förlita sig på cosinuslikhet. Testning i produktionsliknande miljöer före driftsättning är avgörande, särskilt för realtidssystem som API:er och sökmotorer där prestanda och noggrannhet direkt påverkar användarupplevelsen. Populära bibliotek förenklar implementeringen: Scikit-learn erbjuder sklearn.metrics.pairwise.cosine_similarity(), NumPy möjliggör direkt formelimplementering med np.dot() och np.linalg.norm(), TensorFlow och PyTorch erbjuder GPU-accelererade implementationer för storskaliga beräkningar, och PostgreSQL med pgvector ger inbyggda cosinuslikhetsoperatorer för databasfrågor. För organisationer som övervakar AI-omnämnanden och varumärkesnärvaro över plattformar som ChatGPT, Perplexity och Google AI Overviews möjliggör cosinuslikhet exakt spårning av hur AI-system refererar och citerar deras innehåll genom att jämföra frågeinbäddningar mot lagrade varumärkes- och domänvektorer.
Trots dess utbredda användning har cosinuslikhet flera utmaningar som praktiker måste hantera. Måttet är odefinierat för nollvektorer, vilket kräver noggrann datapreprocessing och validering för att undvika körtidsfel. Cosinuslikhet kan ge vilseledande höga likhetspoäng för vektorer som är riktade likadant men semantiskt orelaterade, särskilt när inbäddningsmodeller är dåligt tränade eller när träningsdata saknar mångfald och kontextuell nyans. Denna risk för falsk likhet är särskilt problematisk i applikationer som AI-övervakning där felaktiga likhetsbedömningar kan leda till missade varumärkesomnämnanden eller falska positiva. Måttets symmetri—att det inte kan särskilja jämförelsens ordning—kan vara oönskad i vissa tillämpningar där riktning har betydelse. Dessutom betyder ett cosinuslikhet-värde på 0 inte alltid fullständig olikhet i verkliga sammanhang; i nyanserade domäner som språk kan ortogonala vektorer ändå dela subtila semantiska relationer som måttet inte fångar. Måttets beroende av korrekt normalisering innebär att felaktigt skalad data kan snedvrida resultaten, och organisationer måste säkerställa konsekvent förbehandling av alla vektorer i sina system. Slutligen kan cosinuslikhet ensam vara otillräckligt för komplexa likhetsbedömningar; att kombinera det med andra mått och domänspecifika valideringsregler ger ofta mer robusta resultat.
Cosinuslikhetens roll i AI-system fortsätter att utvecklas i takt med att inbäddningsmodeller blir mer sofistikerade och vektorbaserade arkitekturer dominerar maskininlärning. Framväxande trender inkluderar integration av cosinuslikhet med hybridsökning som kombinerar vektorslikhet med traditionell fulltextsökning, vilket gör det möjligt för system att dra nytta av både semantisk förståelse och nyckelordsmatchning. Multimodala inbäddningar—som representerar text, bilder, ljud och video i ett gemensamt vektorrum—förlitar sig i allt högre grad på cosinuslikhet för att mäta tvärmodala relationer, vilket möjliggör applikationer som bild-till-text-sökning och videoförståelse. Utvecklingen av effektivare approximerade närmaste granne-algoritmer som DiskANN och HNSW fortsätter att förbättra skalbarheten för cosinuslikhets-sökningar, vilket gör semantisk sökning i realtid möjlig i aldrig tidigare skådad skala. Kvantiseringstekniker som minskar vektordimensionalitet samtidigt som cosinuslikhets-relationer bevaras möjliggör implementering av storskalig likhetssökning på edge-enheter och miljöer med begränsade resurser. I sammanhanget AI-övervakning och varumärkesspårning blir cosinuslikhet allt viktigare när organisationer vill förstå hur AI-system som ChatGPT, Perplexity, Claude och Google AI Overviews refererar och citerar deras innehåll. Framtida utveckling kan inkludera adaptiva cosinuslikhetsmått som justerar sitt beteende efter domänspecifika egenskaper, samt integration med förklaringsramverk som hjälper användare att förstå varför vissa vektorer bedöms som lika. I takt med att vektordatabaser mognar och blir standardinfrastruktur för AI-applikationer kommer cosinuslikhet sannolikt att förbli det dominerande måttet för semantisk jämförelse, även om det kan kompletteras med domänspecifika likhetsmått anpassade för specifika applikationer och användningsfall.
För plattformar som AmICited som spårar varumärkes- och domänomnämnanden över AI-system fungerar cosinuslikhet som en kritisk teknisk grund. Vid övervakning av hur ChatGPT, Perplexity, Google AI Overviews och Claude refererar till specifika domäner eller varumärken möjliggör cosinuslikhet exakt mätning av semantisk relevans mellan användarfrågor och AI-svar. Genom att konvertera varumärkesomnämnanden, domän-URL:er och frågeinnehåll till vektorinbäddningar kan cosinuslikhet avgöra om ett AI-svar verkligen citerar eller refererar till ett varumärke jämfört med att bara nämna relaterade begrepp. Denna förmåga är avgörande för organisationer som vill förstå sin synlighet i AI-genererat innehåll och spåra hur deras immateriella rättigheter tillskrivs eller citeras av AI-system. Måttets effektivitet gör det praktiskt för realtidsövervakning av miljontals AI-interaktioner, vilket möjliggör att organisationer får omedelbara aviseringar när deras innehåll refereras. Dessutom möjliggör cosinuslikhet jämförande analys—organisationer kan spåra inte bara om de omnämns, utan även hur deras omnämnandefrekvens och relevans står sig mot konkurrenter, vilket ger konkurrensinformation om AI-systemens beteende och innehållskällor.
Ett cosinuslikhetspoäng på 1 indikerar att två vektorer pekar exakt i samma riktning, vilket betyder att de är perfekt lika. Ett poäng på 0 betyder att vektorerna är ortogonala (vinkelräta), vilket indikerar ingen riktad relation eller likhet. Ett poäng på -1 indikerar att vektorerna pekar i exakt motsatta riktningar, vilket representerar total olikhet. I praktiska NLP-applikationer indikerar poäng närmare 1 semantiskt liknande texter, medan poäng nära 0 tyder på orelaterat innehåll.
Cosinuslikhet föredras för textinbäddningar eftersom den mäter vinkeln mellan vektorer snarare än deras absoluta avstånd, vilket gör den okänslig för vektorns storlek. Detta är avgörande för NLP eftersom dokumentlängd inte bör påverka semantisk likhet—en kort fråga och en lång artikel kan vara lika relevanta. Euklidiskt avstånd är däremot känsligt för storlek och fungerar sämre i högdimensionella rum där vektorer tenderar att konvergera. Cosinuslikhet är också beräkningsmässigt mer effektiv och naturligt begränsad mellan -1 och 1, vilket förhindrar overflow-problem.
I RAG-system driver cosinuslikhet hämtfasen genom att jämföra frågeinbäddningar med dokumentinbäddningar i en vektordatabas. När en användare skickar en fråga konverteras den till en vektor med samma inbäddningsmodell som de lagrade dokumenten. Cosinuslikhet rankar sedan dokumenten efter relevans, där högre poäng indikerar bättre matchningar. De högst rankade dokumenten hämtas och vidarebefordras till LLM:en som kontext, vilket möjliggör mer exakta och faktabaserade svar. Denna process gör att RAG-system kan överbrygga LLM-begränsningar såsom inaktuell kunskap och hallucinationer.
Cosinuslikhet har flera begränsningar: den är odefinierad när vektorer har nollstorlek, vilket kräver förbehandling för att ta bort nollvektorer. Den kan ge vilseledande höga likhetspoäng för vektorer som är riktade likadant men semantiskt orelaterade, särskilt med dåligt tränade inbäddningar. Måttet är också symmetriskt, vilket innebär att det inte kan särskilja ordningen på jämförelsen, vilket kan vara problematiskt i vissa tillämpningar. Dessutom betyder ett likhetspoäng på 0 inte alltid fullständig olikhet i verkliga sammanhang, särskilt i nyanserade domäner som språk där ortogonala vektorer ändå kan dela semantiska relationer.
Cosinuslikhet beräknas med formeln: (A · B) / (||A|| × ||B||), där A · B är skalärprodukten av vektorerna A och B, och ||A|| och ||B|| är deras storlekar (euklidiska normer). Skalärprodukten beräknas genom att multiplicera motsvarande vektorkomponenter och summera resultaten. Vektorns storlek är kvadratroten av summan av dess kvadrerade komponenter. Denna formel ger ett normaliserat poäng mellan -1 och 1, vilket gör det oberoende av vektorns längd och lämpligt för att jämföra vektorer av olika storlek.
I AI-övervakningsplattformar som AmICited är cosinuslikhet avgörande för att spåra varumärkes- och domänomnämnanden över AI-system som ChatGPT, Perplexity och Google AI Overviews. Genom att konvertera varumärkesomnämnanden och frågor till vektorinbäddningar mäter cosinuslikhet hur nära AI-genererade svar stämmer överens med spårat innehåll. Detta gör det möjligt för organisationer att övervaka om deras domäner förekommer i AI-svar, bedöma semantisk relevans för omnämnanden och spåra hur AI-system refererar till deras innehåll jämfört med konkurrenter. Måttets effektivitet gör det praktiskt för realtidsövervakning av miljontals AI-interaktioner.
Stora AI-plattformar och verktyg som utnyttjar cosinuslikhet inkluderar OpenAI:s inbäddningsmodeller, Googles semantiska sökalgoritmer, Perplexitys svarsgenereringssystem och Claudes hämtmekanismer. Vektordatabaser som Pinecone, Weaviate och Milvus använder cosinuslikhet som sitt primära likhetsmått. Öppen källkods-bibliotek som Scikit-learn, TensorFlow, PyTorch och NumPy har inbyggda funktioner för cosinuslikhet. PostgreSQL med pgvector-tillägget möjliggör cosinuslikhetsberäkningar i stor skala. Dessa verktyg driver tillsammans rekommendationssystem, chattbottar, semantiska sökmotorer och RAG-applikationer över hela AI-ekosystemet.
Börja spåra hur AI-chatbotar nämner ditt varumärke på ChatGPT, Perplexity och andra plattformar. Få handlingsbara insikter för att förbättra din AI-närvaro.

Semantisk likhet mäter meningsbaserad närhet mellan texter med hjälp av inbäddningar och avståndsmått. Avgörande för AI-övervakning, innehållsmatchning och varu...

Jämförelseinnehåll jämför flera alternativ för att hjälpa köpare att välja. Lär dig hur detta innehåll med hög köppotential driver konverteringar, bygger auktor...
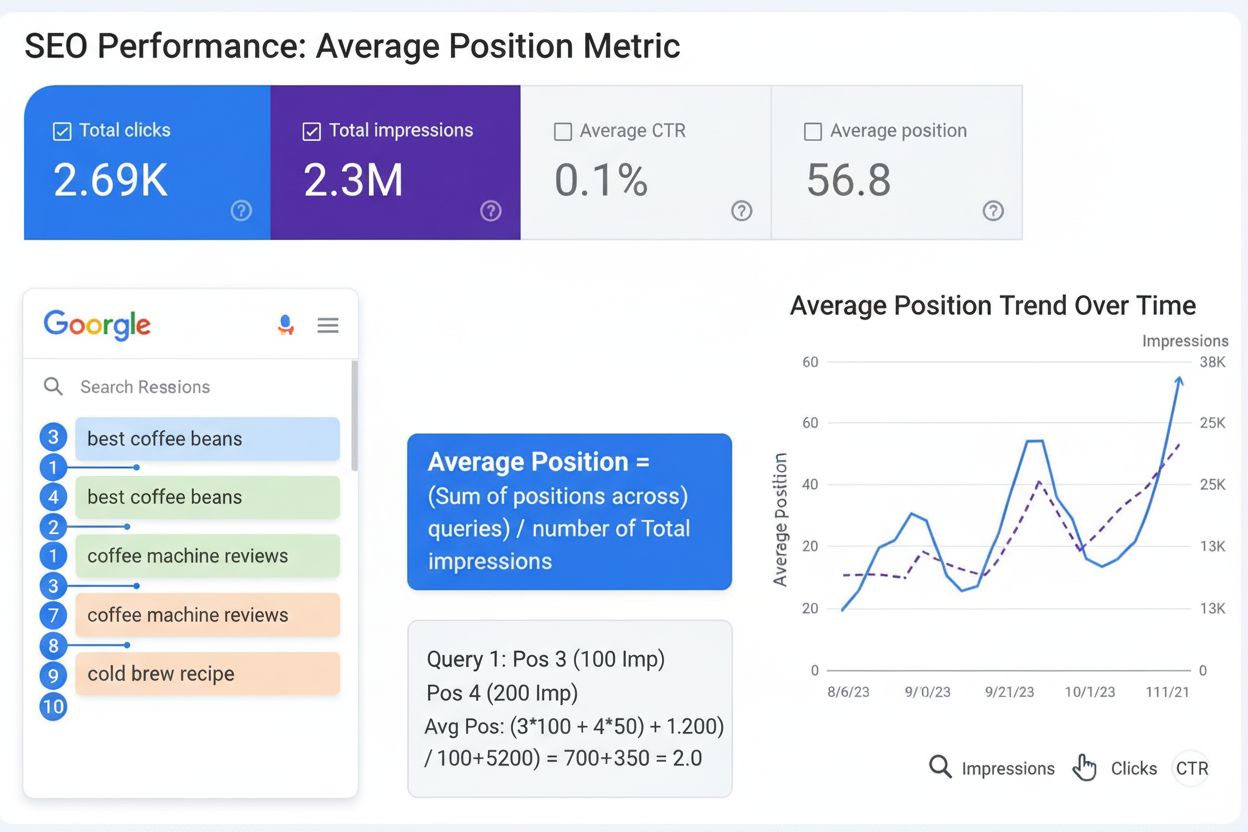
Genomsnittlig position är den genomsnittliga rankningen av din webbsida över sökfrågor. Lär dig hur det beräknas, varför det är viktigt för SEO och hur du använ...
Cookie-samtycke
Vi använder cookies för att förbättra din surfupplevelse och analysera vår trafik. See our privacy policy.