
Sémantická podobnost
Sémantická podobnost měří významovou příbuznost mezi texty pomocí zapouzdření a metrik vzdálenosti. Nezbytné pro AI monitoring, párování obsahu a sledování znač...
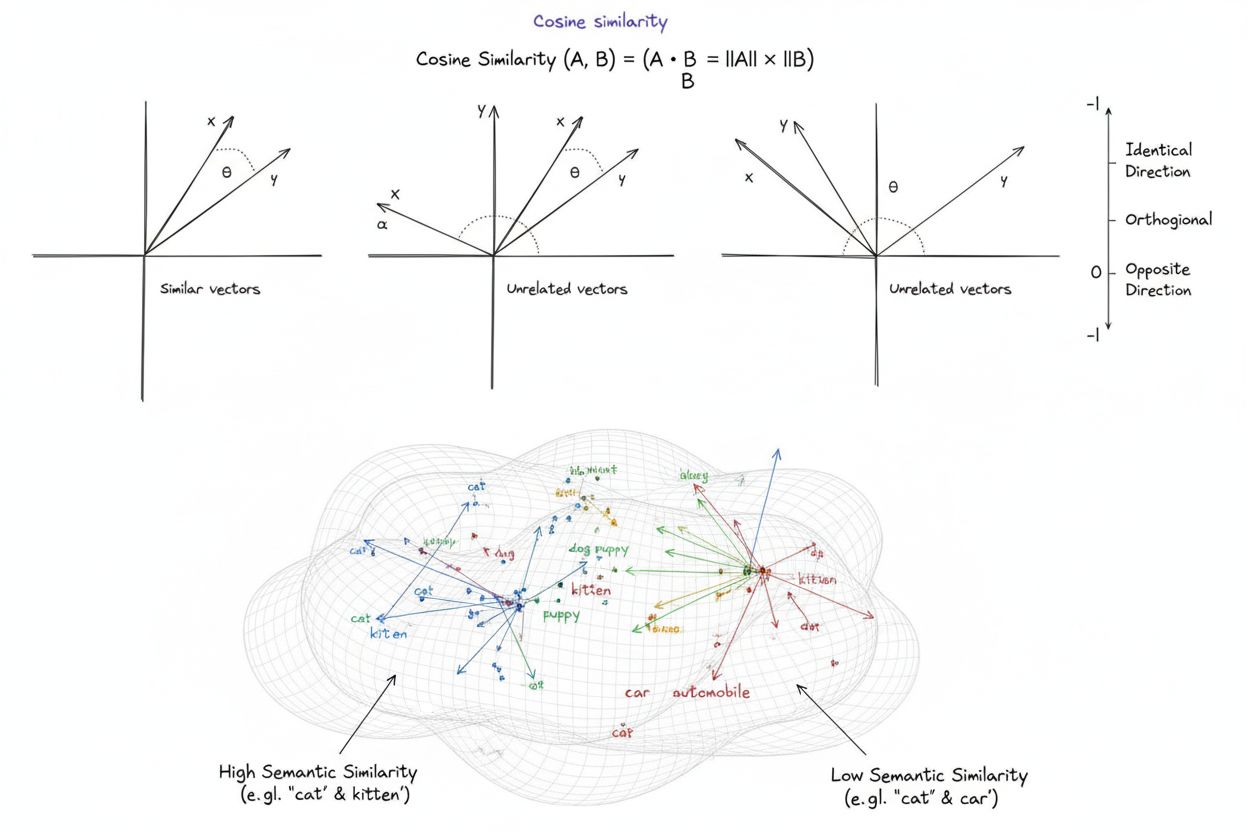
Kosínová podobnost je matematická míra, která vypočítává podobnost mezi dvěma nenulovými vektory určením kosínu úhlu mezi nimi a vytváří skóre v rozmezí od -1 do 1. Široce se používá ve strojovém učení, zpracování přirozeného jazyka a AI systémech k měření sémantické podobnosti mezi textovými embeddingy a vektorovými reprezentacemi, bez ohledu na velikost vektorů.
Kosínová podobnost je matematická míra, která vypočítává podobnost mezi dvěma nenulovými vektory určením kosínu úhlu mezi nimi a vytváří skóre v rozmezí od -1 do 1. Široce se používá ve strojovém učení, zpracování přirozeného jazyka a AI systémech k měření sémantické podobnosti mezi textovými embeddingy a vektorovými reprezentacemi, bez ohledu na velikost vektorů.
Kosínová podobnost je matematická míra, která vypočítává podobnost mezi dvěma nenulovými vektory určením kosínu úhlu mezi nimi ve vícerozměrném prostoru. Metrika vytváří skóre v rozmezí -1 až 1, kde skóre 1 znamená, že vektory směřují zcela stejným směrem, 0 značí ortogonální (kolmé) vektory bez směrového vztahu a -1 znamená, že vektory směřují přesně opačně. V praktických aplikacích je kosínová podobnost zvláště cenná, protože měří směrové zarovnání namísto absolutní vzdálenosti, což ji činí nezávislou na velikosti vektorů. Tato vlastnost je mimořádně užitečná pro porovnávání textových embeddingů, dokumentových vektorů a sémantických reprezentací, kde délka nebo rozsah dat nemá ovlivnit posuzování podobnosti. Metrika se stala základem moderních systémů umělé inteligence, zpracování přirozeného jazyka a strojového učení a pohání vše od vyhledávačů přes doporučovací algoritmy po aplikace velkých jazykových modelů.
Koncept kosínové podobnosti vychází ze základů lineární algebry a trigonometrie, kde kosínus úhlu mezi dvěma vektory poskytuje normalizovanou míru jejich směrového zarovnání. Matematický základ spočívá ve skalárním součinu (vnitřním součinu) vektorů a jejich velikostech, čímž vzniká normalizovaná metrika podobnosti, která je jak výpočetně efektivní, tak teoreticky podložená. Historicky získala kosínová podobnost na významu v oblasti informačního vyhledávání v 70. a 80. letech 20. století, kdy výzkumníci potřebovali efektivní metody pro porovnávání dokumentových vektorů ve velkých textových korpusech. Její rozšíření výrazně zrychlil nástup strojového učení a deep learningu v roce 2010, zejména s tím, jak neurální sítě začaly generovat vysoce dimenzionální vektorové embeddingy pro reprezentaci textu, obrázků a dalších typů dat. Dnes výzkumy ukazují, že více než 78 % podniků implementujících AI systémy využívá kosínovou podobnost nebo příbuzné metriky pro porovnávání vektorů ve svých datových tocích. Matematická elegance metriky – kombinace jednoduchosti a výpočetní efektivity – z ní učinila de facto standard pro měření sémantické podobnosti v NLP aplikacích a hlavní platformy jako OpenAI, Google a Anthropic ji začlenily do svých klíčových systémů.
Výpočet kosínové podobnosti vychází z přesného matematického vzorce: Kosínová podobnost = (A · B) / (||A|| × ||B||), kde A · B představuje skalární součin vektorů A a B a ||A|| a ||B|| jejich příslušné velikosti (Euklidovské normy). Pro výpočet skalárního součinu se vynásobí odpovídající složky obou vektorů a výsledky se sečtou. Například pokud vektor A obsahuje hodnoty [3, 2, 0, 5] a vektor B [1, 0, 0, 0], skalární součin je (3×1) + (2×0) + (0×0) + (5×0) = 3. Velikost vektoru se spočítá jako druhá odmocnina ze součtu druhých mocnin jeho složek; pro vektor A je to √(3² + 2² + 0² + 5²) = √38 ≈ 6,16. Konečné skóre kosínové podobnosti získáte vydělením skalárního součinu součinem velikostí, čímž dostanete normalizovanou hodnotu mezi -1 a 1. Tato normalizace je zásadní, protože činí metriku nezávislou na délce vektoru a umožňuje spravedlivé srovnání vektorů velmi rozdílných měřítek. Ve vysoce dimenzionálních prostorech – například u embeddingů o 1 536 rozměrech produkovaných modelem OpenAI text-embedding-ada-002 – zůstává kosínová podobnost výpočetně nenáročná, protože vyžaduje pouze základní násobení, sčítání a druhou odmocninu, což dnešní procesory zvládnou efektivně i při milionech vektorů.
V zpracování přirozeného jazyka slouží kosínová podobnost jako páteř pro měření sémantických vztahů mezi textovými reprezentacemi. Při převodu textu na vektorové embeddingy pomocí modelů jako BERT, Word2Vec, GloVe nebo embeddingů založených na GPT se každé slovo, fráze či dokument stává bodem ve vysoce dimenzionálním prostoru, kde je sémantika zakódována pozicí a směrem vektoru. Kosínová podobnost pak měří, jak blízko jsou si tyto sémantické reprezentace, což umožňuje systémům pochopit, že například slova „lékař“ a „zdravotní sestra“ jsou sémanticky příbuzná, i když jde o různé pojmy. Tato schopnost je klíčová pro sémantické vyhledávání, kdy je uživatelský dotaz převeden na vektor a porovnán s vektory dokumentů za účelem nalezení nejrelevantnějších výsledků bez ohledu na přesné shody klíčových slov. Ve velkých jazykových modelech jako ChatGPT, Claude a Perplexity pohání kosínová podobnost vyhledávací mechanismy, které získávají relevantní kontext z trénovacích dat či externích znalostních bází. Necitlivost metriky na velikost je zvláště důležitá v NLP, protože délka dokumentu by neměla určovat relevanci – krátký, věcný článek může být sémanticky bližší dotazu než obsáhlý dokument jen díky obsahu. Výzkumy ukazují, že kosínová podobnost překonává alternativní metriky jako euklidovská vzdálenost přibližně v 85 % NLP benchmarků při porovnávání textových embeddingů a je tak preferovanou volbou pro sémantické úlohy v AI průmyslu.
| Metrika | Způsob výpočtu | Rozsah | Citlivost na velikost | Nejlepší použití | Výpočetní složitost |
|---|---|---|---|---|---|
| Kosínová podobnost | (A·B) / ( | A | × | ||
| Euklidovská vzdálenost | √(Σ(Aᵢ - Bᵢ)²) | 0 až ∞ | Ano (závislá na velikosti) | Prostorová data, shlukování, fyzické vzdálenosti | O(n) – efektivní |
| Skalární součin | Σ(Aᵢ × Bᵢ) | -∞ až ∞ | Ano (citlivý na měřítko) | Surové měření podobnosti, není normalizováno | O(n) – velmi efektivní |
| Jaccardova podobnost | |A ∩ B| / |A ∪ B| | 0 až 1 | Ne (množinová) | Kategorická data, doporučovací systémy | O(n) – efektivní |
| Manhattanská vzdálenost | Σ|Aᵢ - Bᵢ| | 0 až ∞ | Ano (závislá na velikosti) | Mřížková data, porovnání vlastností | O(n) – efektivní |
| Pearsonova korelace | Cov(A,B) / (σₐ × σᵦ) | -1 až 1 | Ne (normalizovaná) | Statistické vztahy, časové řady | O(n) – efektivní |
Vektorové databáze jako Pinecone, Weaviate, Milvus a Qdrant představují specializovanou infrastrukturu pro ukládání a vyhledávání vysoce dimenzionálních vektorů s využitím kosínové podobnosti jako hlavní metriky. Tyto databáze jsou optimalizované pro správu milionů či miliard vektorů a umožňují sémantické vyhledávání v reálném čase ve velkém měřítku. Když je do vektorové databáze zadán dotaz, převede se na embedding a porovná se se všemi uloženými vektory pomocí kosínové podobnosti – výsledky jsou seřazeny podle skóre podobnosti. Pro dosažení praktického výkonu u masivních datových sad využívají vektorové databáze algoritmy přibližného nejbližšího souseda (ANN) jako Hierarchical Navigable Small World (HNSW) a DiskANN, které obětují dokonalou přesnost za výrazné zrychlení. Například rozšíření Timescale pgvectorscale, které implementuje StreamingDiskANN, dosahuje 28x nižší latence a 16x vyšší propustnosti dotazů oproti specializovaným vektorovým databázím jako Pinecone, přičemž si zachovává 99% recall při 75% nižších nákladech. V aplikacích sémantického vyhledávání umožňuje kosínová podobnost systémům pochopit uživatelský záměr nad rámec doslovné shody klíčových slov – vyhledání „zdravé stravovací návyky“ vrátí dokumenty o „výživových tipech“ a „vyvážené stravě“, protože jejich embeddingy směřují podobným směrem, i když používají jiné výrazy. Tato schopnost zásadně změnila informační vyhledávání a umožnila vyhledávačům, dokumentačním systémům a znalostním bázím dodávat kontextově relevantní výsledky, které odpovídají uživatelskému záměru, nejen klíčovým slovům.
Retrieval-Augmented Generation (RAG) představuje zásadní změnu v tom, jak velké jazykové modely přistupují k informacím a využívají je, přičemž kosínová podobnost je v této architektuře klíčová. V typickém RAG procesu se při zadání dotazu nejprve převede tento dotaz na vektorový embedding pomocí stejného embedding modelu, jaký se použil pro vektorizaci znalostní báze. Kosínová podobnost pak porovná tento vektor dotazu se všemi dokumentovými vektory ve znalostní bázi a řadí dokumenty podle skóre relevance. Nejvýše hodnocené dokumenty – s nejvyšší kosínovou podobností – jsou načteny a předány LLM jako kontext, na jehož základě je vygenerována odpověď. Tento přístup řeší zásadní omezení samostatných LLM: jejich pevné znalostní uzávěrky, sklony k halucinacím či generování věrohodně znějících, ale nesprávných informací, a nemožnost přístupu k aktuálním nebo proprietárním datům. Díky inteligentnímu vyhledávání pomocí kosínové podobnosti zajišťují RAG systémy, že LLM generuje odpovědi na základě ověřených, aktuálních informací. Mezi hlavní implementace RAG patří OpenAI ChatGPT s pluginy, Anthropic Claude s retrievalem, Google AI Overviews a Perplexity answer generation engine. Výzkumy ukazují, že RAG systémy využívající kosínovou podobnost při vyhledávání zlepšují přesnost odpovědí přibližně o 40–60 % oproti samostatným LLM a zároveň snižují míru halucinací až o 70 %. Efektivita výpočtů kosínové podobnosti je v RAG systémech zásadní, protože musí provádět srovnávání napříč potenciálně miliony dokumentů v reálném čase, a právě výpočetní jednoduchost kosínové podobnosti to umožňuje i ve velkém měřítku.
Efektivní implementace kosínové podobnosti vyžaduje pozornost k několika klíčovým faktorům. Především je nutné předzpracování dat – vektory je třeba před výpočtem normalizovat, aby byla zajištěna konzistence měřítek a správné výsledky, zvláště při práci s vysoce dimenzionálními vstupy z různých zdrojů. Organizace by měly odstranit nebo označit nulové vektory (vektory se samými nulami), protože pro ně není kosínová podobnost matematicky definovaná a při výpočtu by docházelo k dělení nulou. Při implementaci kosínové podobnosti v produkčních systémech se doporučuje kombinovat ji s doplňkovými metrikami, jako je Jaccardova podobnost nebo euklidovská vzdálenost, pokud je třeba posoudit více dimenzí podobnosti – nespoléhat pouze na kosínovou podobnost. Testování v prostředích podobných produkci je klíčové, zejména u systémů v reálném čase, jako jsou API a vyhledávače, kde výkon a přesnost přímo ovlivňují uživatelskou zkušenost. Oblíbené knihovny implementaci usnadňují: Scikit-learn nabízí sklearn.metrics.pairwise.cosine_similarity(), NumPy umožňuje přímou implementaci vzorce s np.dot() a np.linalg.norm(), TensorFlow a PyTorch poskytují GPU-akcelerované implementace pro velké výpočty a PostgreSQL s pgvector nabízí nativní operátory kosínové podobnosti pro dotazy na úrovni databáze. Pro organizace monitorující zmínky AI a přítomnost značky napříč platformami jako ChatGPT, Perplexity a Google AI Overviews umožňuje kosínová podobnost přesně sledovat, jak AI systémy odkazují a citují jejich obsah porovnáním embeddingů dotazů s uloženými vektory značek a domén.
Navzdory širokému rozšíření představuje kosínová podobnost několik výzev, které musí praktici řešit. Metrika není definovaná pro nulové vektory, což vyžaduje důkladné předzpracování dat a validaci, aby se předešlo chybám za běhu. Kosínová podobnost může vést k zavádějícím vysokým skóre u vektorů, které jsou směrově zarovnané, ale sémanticky nesouvisející, zejména pokud jsou embedding modely špatně natrénované nebo pokud tréninková data postrádají rozmanitost a kontext. Riziko falešné podobnosti je obzvlášť problematické v aplikacích typu AI monitoring, kde může nesprávné posouzení podobnosti znamenat přehlédnutí zmínky o značce nebo falešně pozitivní výsledek. Symetričnost metriky – tedy neschopnost rozlišit pořadí porovnání – může být nežádoucí v aplikacích, kde záleží na směru vztahu. Navíc skóre kosínové podobnosti 0 nemusí v reálných situacích znamenat úplnou nepodobnost; v nuancovaných oblastech, jako je jazyk, mohou být ortogonální vektory sémanticky stále příbuzné, což metrika nezachytí. Závislost metriky na správné normalizaci znamená, že špatně škálovaná data mohou výsledky zkreslit a organizace musí zajistit konzistentní předzpracování všech vektorů v systému. Nakonec samotná kosínová podobnost často nestačí pro komplexní posouzení podobnosti; kombinace s dalšími metrikami a doménově specifickými validačními pravidly přináší robustnější výsledky.
Role kosínové podobnosti v AI systémech se vyvíjí s tím, jak embeddingové modely dosahují vyšší sofistikovanosti a vektorové architektury dominují strojovému učení. Mezi nové trendy patří integrace kosínové podobnosti s hybridním vyhledáváním, které kombinuje vektorovou podobnost s tradičním fulltextovým vyhledáváním, takže systémy mohou využívat jak sémantické porozumění, tak shodu klíčových slov. Multimodální embeddingy – které reprezentují text, obrázky, audio i video ve společném vektorovém prostoru – stále častěji využívají kosínovou podobnost pro měření vztahů napříč modalitami, což umožňuje aplikace jako vyhledávání obrázků podle textu či porozumění videím. Rozvoj efektivnějších algoritmů approximate nearest neighbor jako DiskANN a HNSW dále zlepšuje škálovatelnost vyhledávání pomocí kosínové podobnosti a umožňuje sémantické vyhledávání v reálném čase v dosud nevídaném rozsahu. Kvantační techniky snižující dimenzionalitu vektorů při zachování vztahů kosínové podobnosti umožňují nasazení rozsáhlého vyhledávání podobnosti na edge zařízeních a v prostředích s omezenými zdroji. V kontextu AI monitoringu a sledování značky získává kosínová podobnost stále větší význam, protože organizace chtějí vědět, jak systémy jako ChatGPT, Perplexity, Claude a Google AI Overviews odkazují na jejich obsah. Do budoucna se očekává například adaptivní kosínová podobnost, která přizpůsobuje chování doménově specifickým charakteristikám, a integrace s frameworky pro vysvětlitelnost, které uživatelům ukazují, proč byly určité vektory vyhodnoceny jako podobné. S tím, jak vektorové databáze dospívají a stávají se standardní infrastrukturou AI aplikací, zůstane kosínová podobnost pravděpodobně dominantní metrikou pro sémantické porovnávání, byť ji mohou v konkrétních případech doplňovat doménově zaměřené míry podobnosti.
Pro platformy jako AmICited, které sledují zmínky o značkách a doménách napříč AI systémy, je kosínová podobnost klíčovým technickým základem. Při monitoringu, jak ChatGPT, Perplexity, Google AI Overviews a Claude odkazují na konkrétní domény či značky, umožňuje kosínová podobnost přesné měření sémantické relevance mezi uživatelskými dotazy a AI odpověďmi. Převodem zmínek o značce, URL domény a obsahu dotazu na vektorové embeddingy dokáže kosínová podobnost určit, zda odpověď AI systémů opravdu cituje či odkazuje na značku, nebo jen zmiňuje související pojmy. Tato schopnost je nezbytná pro organizace, které chtějí znát svou viditelnost v obsahu generovaném AI a sledovat, jak je jejich duševní vlastnictví AI systémy připisováno či citováno. Efektivita metriky umožňuje praktický monitoring milionů AI interakcí v reálném čase a organizace tak mohou obdržet okamžitá upozornění při zmínkách o jejich obsahu. Navíc umožňuje kosínová podobnost i srovnávací analýzy – organizace mohou sledovat nejen, zda jsou zmiňovány, ale jak se frekvence a relevance zmínek liší oproti konkurenci, což poskytuje konkurenční přehled o chování AI systémů a způsobech získávání obsahu.
Skóre kosínové podobnosti 1 znamená, že oba vektory směřují přesně stejným směrem, tedy jsou dokonale podobné. Skóre 0 znamená, že vektory jsou ortogonální (kolmé), což značí žádný směrový vztah ani podobnost. Skóre -1 znamená, že vektory směřují přesně opačným směrem, což představuje úplnou nepodobnost. V praktických aplikacích NLP skóre blíže 1 naznačuje sémanticky podobné texty, zatímco skóre blízké 0 značí nesouvisející obsah.
Kosínová podobnost je pro textové embeddingy preferovaná, protože měří úhel mezi vektory a ne jejich absolutní vzdálenost, takže je necitlivá na velikost vektoru. To je zásadní pro NLP, protože délka dokumentu by neměla ovlivnit sémantickou podobnost – krátký dotaz a dlouhý článek mohou být stejně relevantní. Euklidovská vzdálenost je naopak citlivá na velikost a v prostředí s vysokou dimenzionalitou, kde se vektory sbíhají, má horší výsledky. Kosínová podobnost je také výpočetně efektivnější a přirozeně omezená mezi -1 a 1, což zabraňuje problémům s přetečením.
V systémech RAG pohání kosínová podobnost fázi vyhledávání porovnáváním embeddingů dotazu s embeddingy dokumentů ve vektorové databázi. Když uživatel zadá dotaz, je převeden na vektor pomocí stejného embedding modelu jako uložené dokumenty. Kosínová podobnost pak řadí dokumenty podle relevance, přičemž vyšší skóre značí lepší shodu. Nejlépe hodnocené dokumenty jsou načteny a předány LLM jako kontext, což umožňuje přesnější a věcně podložené odpovědi. Tento proces umožňuje systémům RAG překonat omezení LLM, jako jsou zastaralé znalosti a halucinace.
Kosínová podobnost má několik omezení: není definovaná pro vektory s nulovou velikostí, což vyžaduje předzpracování a odstranění nulových vektorů. Může vést k zavádějícím vysokým skóre pro směrově zarovnané, ale sémanticky nesouvisející vektory, zvláště při špatně natrénovaných embeddingech. Metrika je také symetrická, takže nerozlišuje pořadí porovnání, což může být problém v některých aplikacích. Navíc skóre podobnosti 0 nemusí vždy znamenat úplnou nepodobnost v reálných situacích, zejména v nuancovaných oblastech, jako je jazyk, kde ortogonální vektory mohou sdílet sémantické vztahy.
Kosínová podobnost se vypočítá podle vzorce: (A · B) / (||A|| × ||B||), kde A · B je skalární součin vektorů A a B a ||A|| a ||B|| jsou jejich velikosti (Euklidovské normy). Skalární součin se spočítá vynásobením odpovídajících složek vektorů a sečtením výsledků. Velikost vektoru je druhá odmocnina ze součtu druhých mocnin jeho složek. Tento vzorec vrací normalizované skóre mezi -1 a 1, což jej činí nezávislým na délce vektoru a vhodným pro porovnávání vektorů různých velikostí.
V AI monitorovacích platformách jako AmICited je kosínová podobnost klíčová pro sledování zmínek o značce a doméně napříč AI systémy jako ChatGPT, Perplexity a Google AI Overviews. Převodem zmínek o značce a dotazů na vektorové embeddingy měří kosínová podobnost, jak moc odpovědi generované AI odpovídají sledovanému obsahu. To umožňuje organizacím sledovat, zda se jejich domény objevují v AI odpovědích, hodnotit sémantickou relevanci zmínek a porovnávat, jak AI systémy odkazují na jejich obsah oproti konkurenci. Efektivita metriky umožňuje monitorování milionů AI interakcí v reálném čase.
Hlavní AI platformy a nástroje využívající kosínovou podobnost zahrnují embedding modely OpenAI, sémantické vyhledávací algoritmy Google, systém generování odpovědí Perplexity a vyhledávací mechanismy Claude. Vektorové databáze jako Pinecone, Weaviate a Milvus používají kosínovou podobnost jako hlavní metriku podobnosti. Open-source knihovny jako Scikit-learn, TensorFlow, PyTorch a NumPy mají vestavěné funkce pro kosínovou podobnost. PostgreSQL s rozšířením pgvector umožňuje výpočty kosínové podobnosti ve velkém měřítku. Tyto nástroje pohánějí doporučovací systémy, chatboty, sémantické vyhledávače i RAG aplikace v rámci AI ekosystému.
Začněte sledovat, jak AI chatboti zmiňují vaši značku na ChatGPT, Perplexity a dalších platformách. Získejte užitečné informace pro zlepšení vaší AI prezence.

Sémantická podobnost měří významovou příbuznost mezi texty pomocí zapouzdření a metrik vzdálenosti. Nezbytné pro AI monitoring, párování obsahu a sledování znač...
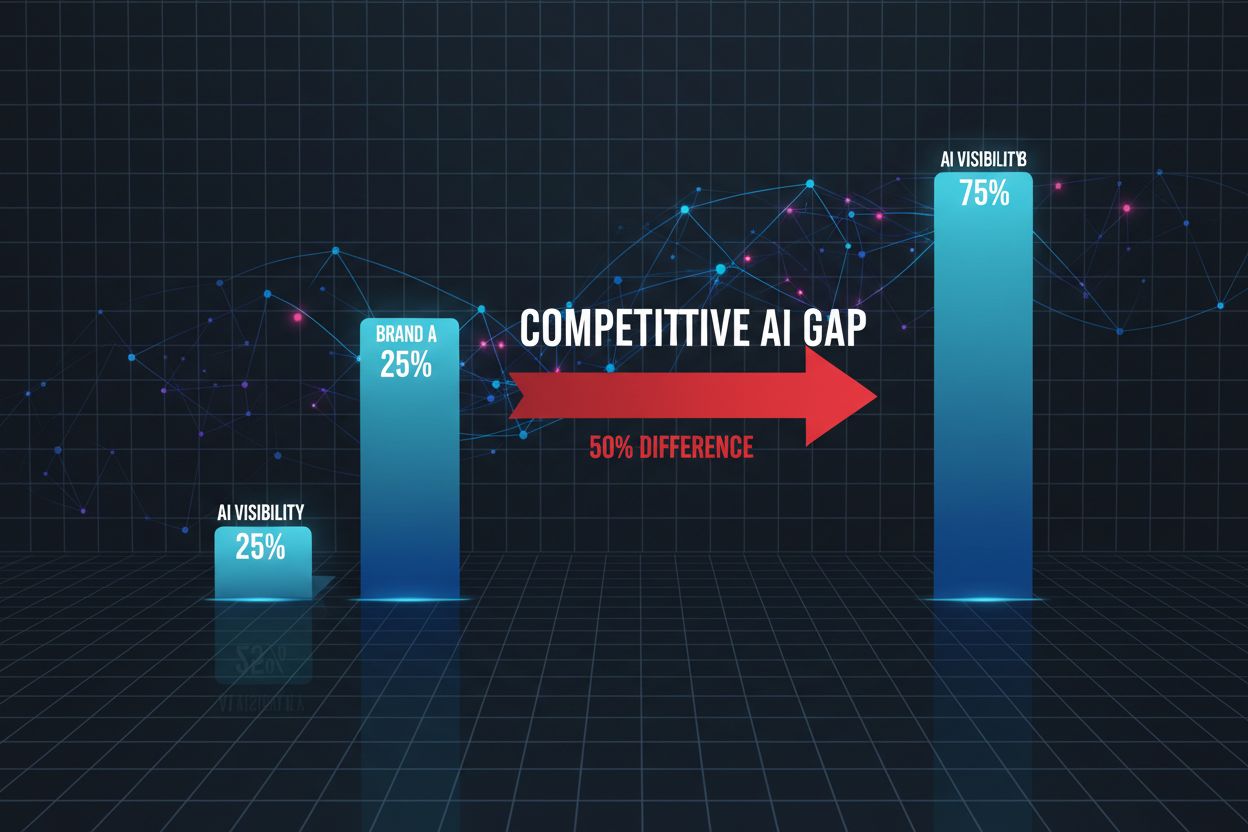
Zjistěte, co znamená konkurenční AI mezera, jak ji měřit a proč je důležitá pro viditelnost vaší značky v ChatGPT, Claude, Gemini a dalších AI systémech. Objevt...
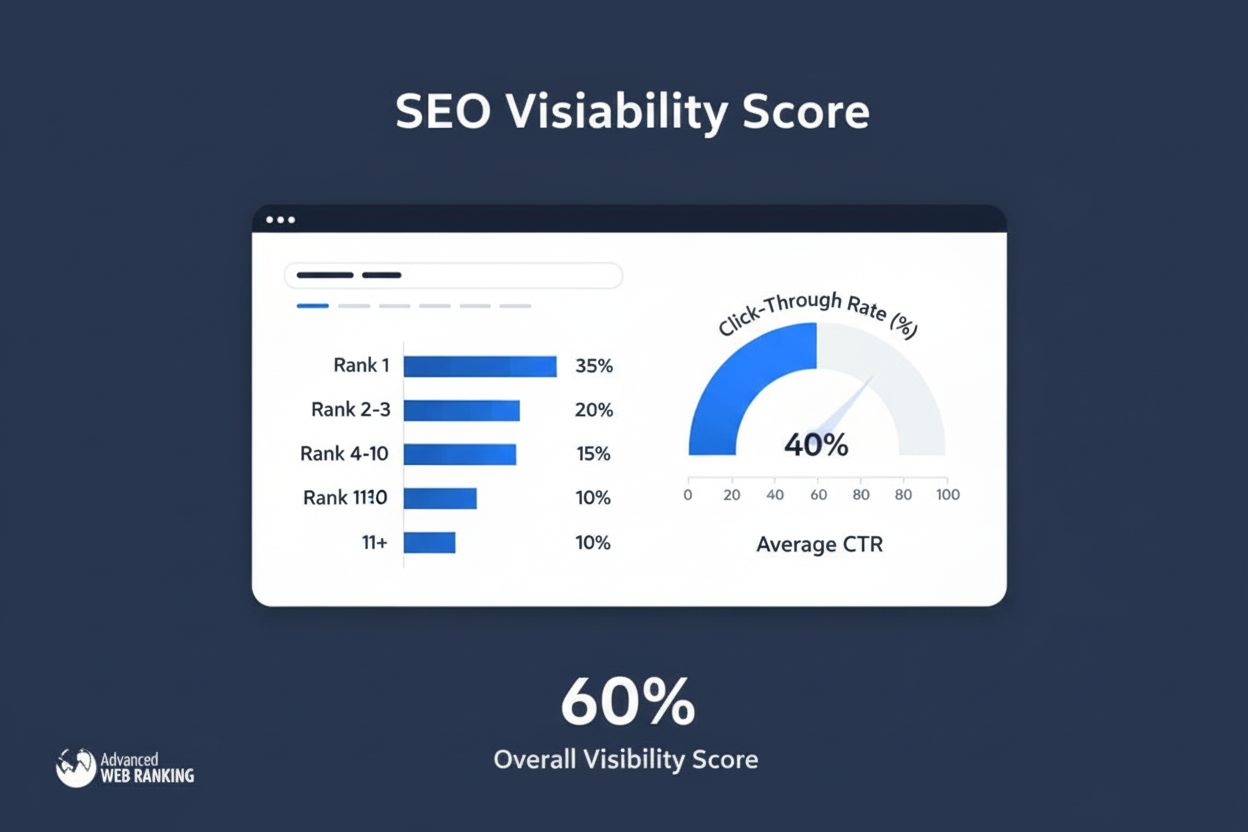
Skóre viditelnosti měří vyhledávací přítomnost výpočtem odhadovaných kliknutí z organických pozic. Zjistěte, jak tato metrika funguje, metody výpočtu a proč je ...
Souhlas s cookies
Používáme cookies ke zlepšení vašeho prohlížení a analýze naší návštěvnosti. See our privacy policy.