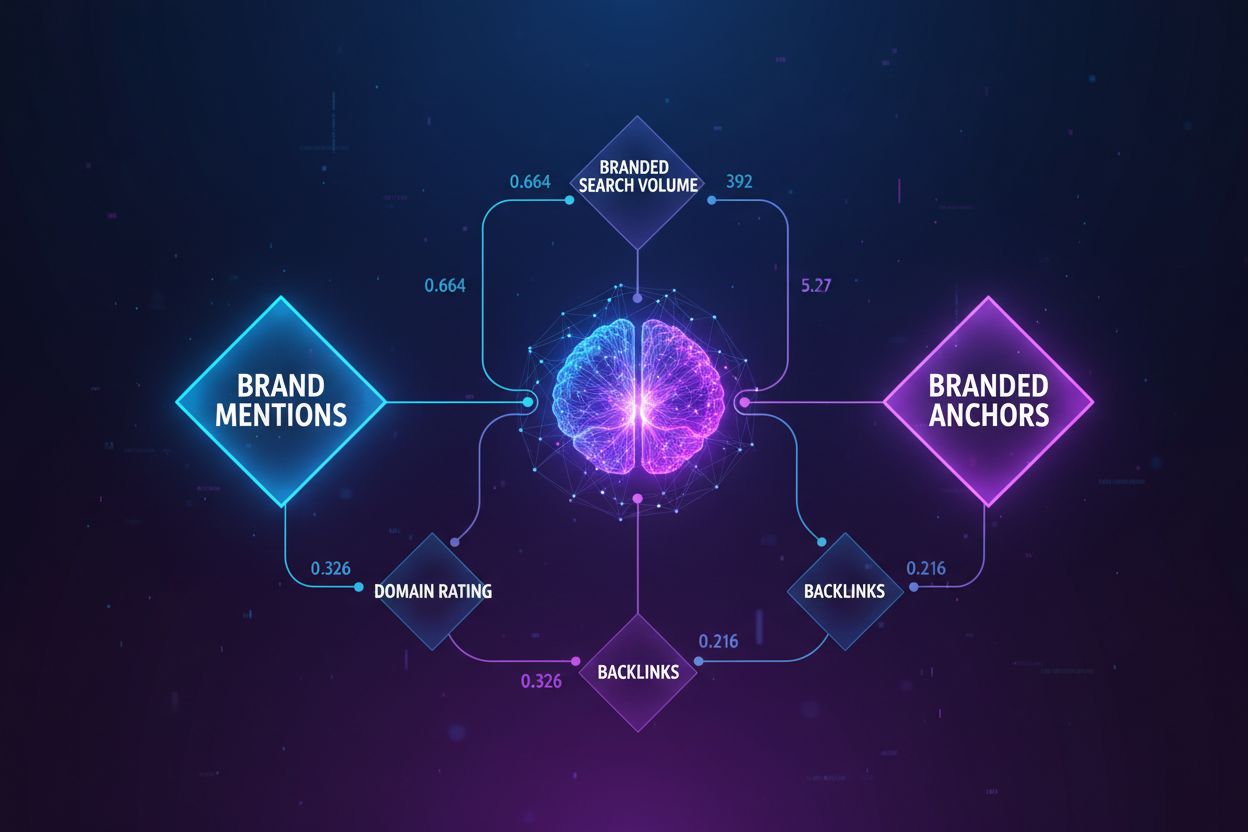
Korrelationsanalyse: Faktoren, die Ihre KI-Sichtbarkeit bestimmen
Entdecken Sie, welche Faktoren am stärksten mit der KI-Sichtbarkeit korrelieren. Erfahren Sie, wie Marken-Nennungen, Suchvolumen und Ankertexte die KI Overviews...
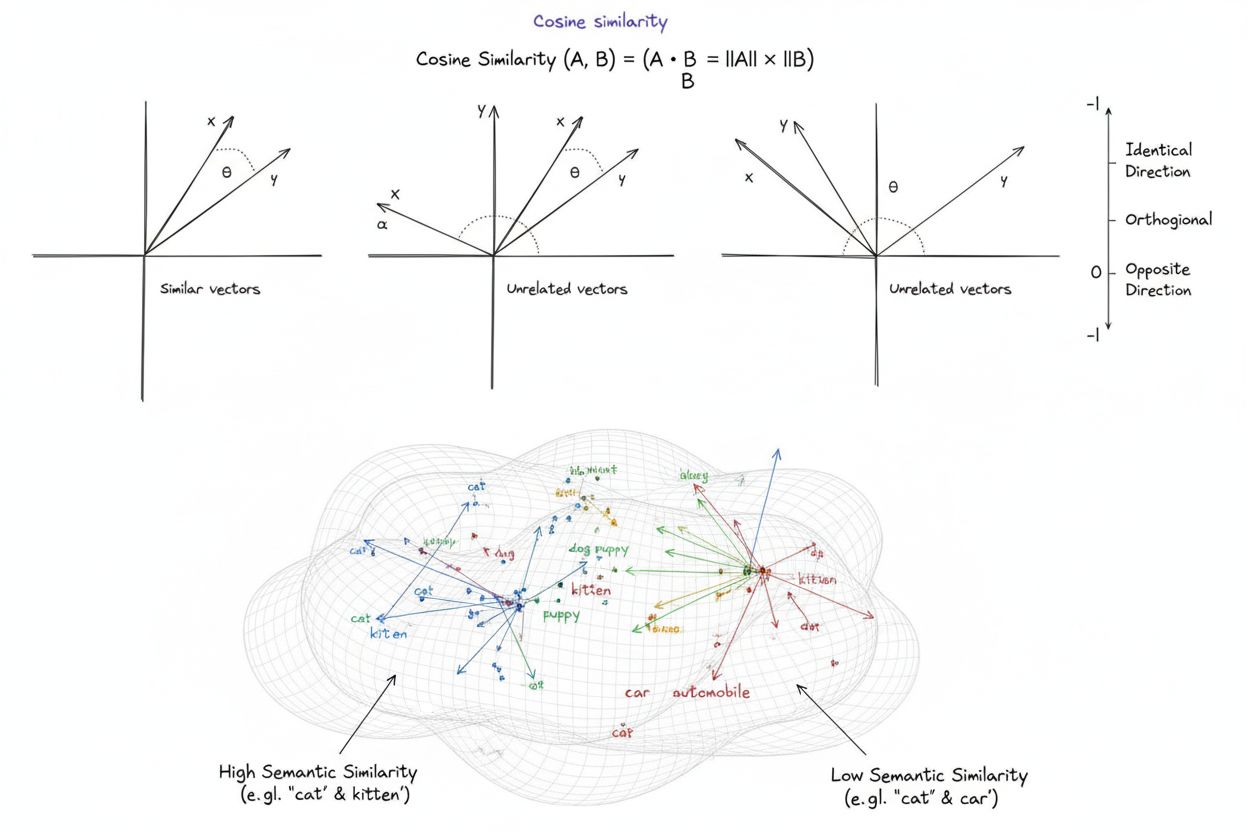
Die Kosinus-Ähnlichkeit ist ein mathematisches Maß, das die Ähnlichkeit zwischen zwei von null verschiedenen Vektoren berechnet, indem der Kosinus des Winkels zwischen ihnen bestimmt wird. Das Ergebnis ist ein Wert im Bereich von -1 bis 1. Sie wird häufig im maschinellen Lernen, in der Verarbeitung natürlicher Sprache und in KI-Systemen eingesetzt, um semantische Ähnlichkeit zwischen Text-Embeddings und Vektorrepräsentationen zu messen – unabhängig von der Vektorlänge.
Die Kosinus-Ähnlichkeit ist ein mathematisches Maß, das die Ähnlichkeit zwischen zwei von null verschiedenen Vektoren berechnet, indem der Kosinus des Winkels zwischen ihnen bestimmt wird. Das Ergebnis ist ein Wert im Bereich von -1 bis 1. Sie wird häufig im maschinellen Lernen, in der Verarbeitung natürlicher Sprache und in KI-Systemen eingesetzt, um semantische Ähnlichkeit zwischen Text-Embeddings und Vektorrepräsentationen zu messen – unabhängig von der Vektorlänge.
Kosinus-Ähnlichkeit ist ein mathematisches Maß, das die Ähnlichkeit zwischen zwei von null verschiedenen Vektoren berechnet, indem der Kosinus des Winkels zwischen ihnen in einem mehrdimensionalen Raum bestimmt wird. Das Maß liefert einen Wert im Bereich von -1 bis 1, wobei 1 anzeigt, dass die Vektoren in identische Richtungen zeigen, 0 für orthogonale (rechtwinklige) Vektoren ohne richtungsbezogene Beziehung steht und -1 bedeutet, dass die Vektoren in genau entgegengesetzte Richtungen zeigen. In der Praxis ist die Kosinus-Ähnlichkeit besonders wertvoll, weil sie die Ausrichtung (Richtung) und nicht die absolute Entfernung misst und somit unabhängig von der Vektorlänge ist. Diese Eigenschaft macht sie besonders nützlich für den Vergleich von Text-Embeddings, Dokumentenvektoren und semantischen Repräsentationen, bei denen die Länge oder Skalierung der Daten die Ähnlichkeitsbewertung nicht beeinflussen sollte. Das Maß ist grundlegend für moderne künstliche Intelligenz, Verarbeitung natürlicher Sprache und maschinelles Lernen und treibt alles an – von Suchmaschinen über Empfehlungssysteme bis hin zu Anwendungen großer Sprachmodelle.
Das Konzept der Kosinus-Ähnlichkeit stammt aus der linearen Algebra und Trigonometrie, bei der der Kosinus des Winkels zwischen zwei Vektoren ein normalisiertes Maß für deren Richtungsübereinstimmung liefert. Die mathematische Grundlage basiert auf dem Skalarprodukt (inneres Produkt) von Vektoren und deren Beträgen, was ein normalisiertes, recheneffizientes und theoretisch fundiertes Ähnlichkeitsmaß ergibt. Historisch gewann die Kosinus-Ähnlichkeit in der Informationssuche in den 1970er und 1980er Jahren an Bedeutung, als Forscher nach effizienten Methoden suchten, um Dokumentenvektoren in großen Textkorpora zu vergleichen. Mit dem Aufstieg von maschinellem Lernen und Deep Learning in den 2010er Jahren – insbesondere als neuronale Netze hochdimensionale Vektorembeddings zur Repräsentation von Text, Bildern und anderen Datentypen erzeugten – beschleunigte sich die Verbreitung des Maßes enorm. Heute zeigen Untersuchungen, dass über 78 % der Unternehmen, die KI-basierte Systeme einführen, Kosinus-Ähnlichkeit oder verwandte Vektorvergleichsmetriken in ihren Datenpipelines nutzen. Die mathematische Eleganz dieses Maßes – die Einfachheit mit rechnerischer Effizienz verbindet – hat es zum Standard für die Messung semantischer Ähnlichkeit in NLP-Anwendungen gemacht. Große Plattformen wie OpenAI, Google und Anthropic setzen es in ihren zentralen Systemen ein.
Die Berechnung der Kosinus-Ähnlichkeit folgt einer exakten mathematischen Formel: Kosinus-Ähnlichkeit = (A · B) / (||A|| × ||B||), wobei A · B das Skalarprodukt der Vektoren A und B ist und ||A|| sowie ||B|| ihre Beträge (euklidische Normen) darstellen. Für das Skalarprodukt werden die entsprechenden Komponenten der beiden Vektoren multipliziert und die Produkte aufsummiert. Beispiel: Wenn Vektor A die Werte [3, 2, 0, 5] und Vektor B [1, 0, 0, 0] enthält, ergibt das Skalarprodukt (3×1) + (2×0) + (0×0) + (5×0) = 3. Die Länge eines Vektors berechnet sich als Quadratwurzel der Summe seiner quadrierten Komponenten; für A also √(3² + 2² + 0² + 5²) = √38 ≈ 6,16. Der finale Kosinus-Ähnlichkeitswert wird berechnet, indem das Skalarprodukt durch das Produkt der Beträge geteilt wird, was einen normalisierten Wert zwischen -1 und 1 ergibt. Diese Normalisierung ist entscheidend, da das Maß unabhängig von der Vektorlänge ist und faire Vergleiche unabhängig von der Skalierung der Vektoren ermöglicht. In hochdimensionalen Räumen – wie den 1.536-dimensionalen Embeddings des OpenAI-Modells text-embedding-ada-002 – bleibt die Kosinus-Ähnlichkeit rechenbar, da nur Multiplikation, Addition und Quadratwurzel benötigt werden, was moderne Prozessoren auch für Millionen von Vektoren effizient ausführen können.
In der Verarbeitung natürlicher Sprache bildet die Kosinus-Ähnlichkeit das Rückgrat bei der Messung semantischer Beziehungen zwischen Textrepräsentationen. Wenn Text mit Modellen wie BERT, Word2Vec, GloVe oder GPT-basierten Embeddings in Vektorembeddings umgewandelt wird, stellt jedes Wort, jede Phrase oder jedes Dokument einen Punkt im hochdimensionalen Raum dar, wobei die semantische Bedeutung durch die Position und Richtung des Vektors kodiert ist. Die Kosinus-Ähnlichkeit misst dann, wie eng diese semantischen Repräsentationen übereinstimmen, sodass Systeme erkennen können, dass z. B. “Arzt” und “Krankenschwester” semantisch verwandt sind, obwohl die Begriffe unterschiedlich sind. Diese Fähigkeit ist essenziell für die semantische Suche, bei der eine Nutzeranfrage in einen Vektor konvertiert und mit Dokumentenvektoren verglichen wird, um die relevantesten Ergebnisse unabhängig von exakter Stichwortübereinstimmung zu finden. In großen Sprachmodellen wie ChatGPT, Claude und Perplexity steuert die Kosinus-Ähnlichkeit die Retrieval-Mechanismen, die relevanten Kontext aus Trainingsdaten oder externen Wissensquellen holen. Die Unempfindlichkeit gegenüber der Vektorlänge ist besonders wichtig, da die Dokumentlänge nicht die Relevanz bestimmen sollte – ein kurzer, prägnanter Artikel kann semantisch ähnlicher zur Anfrage sein als ein langer Text, einfach aufgrund seines Inhalts. Studien zeigen, dass die Kosinus-Ähnlichkeit alternative Maße wie die euklidische Distanz in etwa 85 % der NLP-Benchmarks beim Vergleich von Text-Embeddings übertrifft und somit die bevorzugte Wahl für semantische Aufgaben in der KI-Branche ist.
| Metrik | Berechnungsmethode | Wertebereich | Empfindlichkeit gegenüber der Vektorlänge | Bester Anwendungsfall | Rechenaufwand |
|---|---|---|---|---|---|
| Kosinus-Ähnlichkeit | (A·B) / ( | A | × | ||
| Euklidische Distanz | √(Σ(Aᵢ - Bᵢ)²) | 0 bis ∞ | Ja (längenabhängig) | Räumliche Daten, Clustering, physische Distanzen | O(n) – effizient |
| Skalarprodukt | Σ(Aᵢ × Bᵢ) | -∞ bis ∞ | Ja (skalenabhängig) | Rohe Ähnlichkeitsmessung, nicht normalisiert | O(n) – sehr effizient |
| Jaccard-Ähnlichkeit | |A ∩ B| / |A ∪ B| | 0 bis 1 | Nein (mengenbasiert) | Kategorische Daten, Empfehlungssysteme | O(n) – effizient |
| Manhattan-Distanz | Σ|Aᵢ - Bᵢ| | 0 bis ∞ | Ja (längenabhängig) | Gitterbasierte Daten, Merkmalsvergleich | O(n) – effizient |
| Pearson-Korrelation | Cov(A,B) / (σₐ × σᵦ) | -1 bis 1 | Nein (normalisiert) | Statistische Beziehungen, Zeitreihen | O(n) – effizient |
Vektordatenbanken wie Pinecone, Weaviate, Milvus und Qdrant sind als spezialisierte Infrastrukturen für das Speichern und Abfragen hochdimensionaler Vektoren mit der Kosinus-Ähnlichkeit als Hauptmaß entstanden. Diese Datenbanken sind darauf optimiert, Millionen oder Milliarden von Vektoren zu verwalten und ermöglichen semantische Echtzeitsuche im großen Maßstab. Bei einer Suchanfrage wird diese in ein Embedding umgewandelt und mit allen gespeicherten Vektoren mittels Kosinus-Ähnlichkeit verglichen; die Ergebnisse werden nach Ähnlichkeitswert sortiert. Um eine hohe Performance bei riesigen Datenmengen zu erreichen, setzen Vektordatenbanken Approximate Nearest Neighbor (ANN)-Algorithmen wie Hierarchical Navigable Small World (HNSW) und DiskANN ein, die zugunsten von Geschwindigkeit auf perfekte Genauigkeit verzichten. Beispielsweise erzielt die pgvectorscale-Erweiterung von Timescale, die StreamingDiskANN implementiert, eine 28-fach geringere Latenz und 16-fach höhere Abfrageleistung als spezialisierte Vektordatenbanken wie Pinecone – bei 99 % Recall und 75 % geringeren Kosten. In semantischen Suchanwendungen ermöglicht die Kosinus-Ähnlichkeit Systemen, Benutzerintentionen über wörtliche Stichwortsuche hinaus zu erfassen – eine Suche nach “gesunde Essgewohnheiten” findet etwa auch Dokumente zu “Ernährungstipps” und “ausgewogene Ernährung”, da deren Embeddings in ähnliche Richtungen zeigen, obwohl andere Begriffe verwendet werden. Diese Fähigkeit hat die Informationssuche revolutioniert und ermöglicht Suchmaschinen, Dokumentationssystemen und Wissensdatenbanken, kontextuell relevante und nicht nur stichwortgleiche Ergebnisse zu liefern.
Retrieval-Augmented Generation (RAG) ist ein Paradigmenwechsel für den Zugriff und die Nutzung von Informationen durch große Sprachmodelle, wobei die Kosinus-Ähnlichkeit das Kernstück dieser Architektur bildet. In einer typischen RAG-Pipeline wird die Nutzeranfrage zunächst mit demselben Embedding-Modell wie die Wissensdatenbank in einen Vektor konvertiert. Die Kosinus-Ähnlichkeit vergleicht diesen Abfragevektor mit allen Dokumentenvektoren der Wissensdatenbank und ordnet die Dokumente nach Relevanzwert. Die am höchsten bewerteten Dokumente – also jene mit dem höchsten Kosinus-Ähnlichkeitswert – werden abgerufen und als Kontext an das LLM übergeben, das darauf basierende Antworten generiert. Damit werden zentrale Schwächen von reinen LLMs adressiert: begrenzter Wissensstand, Gefahr von Halluzinationen oder scheinbar plausiblen, aber falschen Informationen sowie der fehlende Zugriff auf aktuelle oder proprietäre Daten. Durch die intelligente Auswahl auf Basis der Kosinus-Ähnlichkeit sorgen RAG-Systeme dafür, dass LLMs Antworten auf Basis verifizierter und aktueller Informationen generieren. Bedeutende Implementierungen sind etwa OpenAI ChatGPT mit Plugins, Claude mit Retrieval von Anthropic, Google AI Overviews und die Antwortgenerierung von Perplexity. Studien zeigen, dass RAG-Systeme mit Kosinus-Ähnlichkeit die Antwortgenauigkeit im Vergleich zu reinen LLMs um etwa 40–60 % steigern und die Halluzinationsrate um bis zu 70 % senken. Die Recheneffizienz der Kosinus-Ähnlichkeit ist besonders für RAG-Systeme relevant, da oft Millionen von Dokumenten in Echtzeit verglichen werden müssen – und gerade die Einfachheit der Berechnung macht dies im großen Maßstab möglich.
Für die effektive Implementierung der Kosinus-Ähnlichkeit sind mehrere Faktoren entscheidend. Zunächst ist eine Datenvorverarbeitung unerlässlich – Vektoren müssen vor der Berechnung normalisiert werden, um einheitliche Skalierung und gültige Ergebnisse sicherzustellen, insbesondere bei hochdimensionalen Eingaben aus verschiedenen Quellen. Nullvektoren (Vektoren mit nur Nullen) sollten entfernt oder gekennzeichnet werden, da die Kosinus-Ähnlichkeit mathematisch nicht für Nullvektoren definiert ist und sonst Division-durch-Null-Fehler verursachen kann. In produktiven Systemen empfiehlt es sich, die Kosinus-Ähnlichkeit mit ergänzenden Metriken wie Jaccard-Ähnlichkeit oder euklidischer Distanz zu kombinieren, wenn mehrere Dimensionen der Ähnlichkeit relevant sind, anstatt sich ausschließlich auf die Kosinus-Ähnlichkeit zu verlassen. Vor dem Einsatz in Echtzeit-Systemen wie APIs und Suchmaschinen sollte in produktionsnahen Umgebungen getestet werden, da Performance und Genauigkeit das Nutzererlebnis direkt beeinflussen. Beliebte Bibliotheken erleichtern die Implementierung: Scikit-learn bietet sklearn.metrics.pairwise.cosine_similarity(), NumPy die direkte Formelumsetzung mit np.dot() und np.linalg.norm(), TensorFlow und PyTorch liefern GPU-beschleunigte Implementierungen für große Datenmengen, und PostgreSQL mit pgvector ermöglicht Kosinus-Operatoren auf Datenbankebene. Für Unternehmen, die KI-Erwähnungen oder Markenpräsenz auf Plattformen wie ChatGPT, Perplexity und Google AI Overviews überwachen, ermöglicht die Kosinus-Ähnlichkeit eine präzise Nachverfolgung, wie KI-Systeme Inhalte referenzieren, indem Abfrage-Embeddings mit gespeicherten Marken- und Domainvektoren verglichen werden.
Trotz ihrer weiten Verbreitung bringt die Kosinus-Ähnlichkeit einige Herausforderungen mit sich. Das Maß ist für Nullvektoren nicht definiert, weshalb eine sorgfältige Datenvorverarbeitung und Validierung nötig ist, um Laufzeitfehler zu vermeiden. Kosinus-Ähnlichkeit kann irreführend hohe Werte für Richtungsübereinstimmungen liefern, die semantisch jedoch nicht zusammenhängen, insbesondere wenn Embedding-Modelle schlecht trainiert wurden oder das Trainingsmaterial wenig Vielfalt und Kontexttiefe aufweist. Diese Gefahr von falscher Ähnlichkeit ist besonders bei KI-Monitoring-Anwendungen problematisch, bei denen fehlerhafte Bewertungen zu verpassten Marken-Erwähnungen oder Fehlalarmen führen können. Die Symmetrie des Maßes – also die Unempfindlichkeit gegenüber der Vergleichsrichtung – kann in Anwendungen unerwünscht sein, bei denen die Richtung eine Rolle spielt. Außerdem bedeutet ein Wert von 0 nicht zwingend vollständige Unähnlichkeit im realen Kontext; in Sprachdomänen können orthogonale Vektoren dennoch subtile semantische Beziehungen haben, die das Maß nicht erfasst. Die Abhängigkeit von ordnungsgemäßer Normalisierung kann zu verzerrten Ergebnissen führen, wenn Daten nicht konsistent vorverarbeitet werden. Schließlich reicht die Kosinus-Ähnlichkeit allein für komplexe Ähnlichkeitsbewertungen oft nicht aus; eine Kombination mit anderen Metriken und domänenspezifischen Validierungsregeln liefert meist robustere Resultate.
Die Rolle der Kosinus-Ähnlichkeit in KI-Systemen entwickelt sich weiter, je komplexer Embedding-Modelle und vektorbasierte Architekturen werden. Zu den aktuellen Trends gehört die Integration von Kosinus-Ähnlichkeit mit hybriden Suchansätzen, die Vektorähnlichkeit und klassische Volltextsuche kombinieren und so sowohl semantisches Verständnis als auch Stichwortsuche ermöglichen. Multimodale Embeddings – die Text, Bilder, Audio und Video gemeinsam im Vektorraum abbilden – verlassen sich zunehmend auf die Kosinus-Ähnlichkeit zur Messung von Beziehungen zwischen verschiedenen Modalitäten, z. B. für Bild-zu-Text-Suche und Videoanalyse. Die Entwicklung effizienterer ANN-Algorithmen wie DiskANN und HNSW verbessert die Skalierbarkeit der Kosinus-Ähnlichkeit weiter und macht semantische Suche in Echtzeit auch bei extremen Datenmengen möglich. Quantisierungstechniken, die die Vektordimension verringern, ohne die Kosinus-Ähnlichkeit wesentlich zu beeinflussen, erlauben den Einsatz von Ähnlichkeitssuche sogar auf Edge-Geräten und in ressourcenbeschränkten Umgebungen. Im Kontext von KI-Monitoring und Markenbeobachtung wird die Kosinus-Ähnlichkeit immer wichtiger, da Unternehmen verstehen möchten, wie Systeme wie ChatGPT, Perplexity, Claude und Google AI Overviews ihre Inhalte zitieren und referenzieren. Zukünftige Entwicklungen könnten adaptive Kosinus-Ähnlichkeitsmetriken umfassen, die ihr Verhalten an domänenspezifische Besonderheiten anpassen, sowie die Integration in Erklärbarkeits-Frameworks, die Nutzern helfen, die Gründe für bestimmte Ähnlichkeitsbewertungen nachzuvollziehen. Mit der zunehmenden Standardisierung von Vektordatenbanken für KI-Anwendungen bleibt die Kosinus-Ähnlichkeit voraussichtlich das dominierende Maß für semantische Vergleiche, auch wenn sie durch spezielle domänenspezifische Metriken ergänzt werden könnte.
Für Plattformen wie AmICited, die Marken- und Domain-Erwähnungen in KI-Systemen verfolgen, ist die Kosinus-Ähnlichkeit eine zentrale technische Grundlage. Beim Monitoring, wie ChatGPT, Perplexity, Google AI Overviews und Claude bestimmte Domains oder Marken referenzieren, ermöglicht die Kosinus-Ähnlichkeit eine präzise Messung der semantischen Relevanz zwischen Nutzeranfragen und KI-Antworten. Durch die Umwandlung von Marken-Erwähnungen, Domain-URLs und Abfrageinhalten in Vektorembeddings kann die Kosinus-Ähnlichkeit bestimmen, ob eine KI-Antwort tatsächlich eine Marke zitiert oder nur verwandte Begriffe erwähnt. Diese Fähigkeit ist für Unternehmen essenziell, die ihre Sichtbarkeit in KI-generierten Inhalten verstehen und nachvollziehen möchten, wie ihr geistiges Eigentum von KI-Systemen referenziert oder zitiert wird. Die Effizienz des Maßes ermöglicht die Echtzeitüberwachung von Millionen KI-Interaktionen, sodass Unternehmen sofort benachrichtigt werden, wenn ihre Inhalte genannt werden. Darüber hinaus unterstützt die Kosinus-Ähnlichkeit den Wettbewerbsvergleich – Unternehmen können nicht nur verfolgen, ob sie erwähnt werden, sondern auch, wie Häufigkeit und Relevanz der Erwähnungen im Vergleich zu Mitbewerbern ausfallen. Das liefert wertvolle Einblicke in das Verhalten und die Quellenwahl von KI-Systemen.
Ein Kosinus-Ähnlichkeitswert von 1 zeigt an, dass zwei Vektoren exakt in die gleiche Richtung zeigen, sie sind also vollkommen ähnlich. Ein Wert von 0 bedeutet, dass die Vektoren orthogonal (rechtwinklig) zueinander stehen, was auf keine richtungsbezogene Beziehung oder Ähnlichkeit hindeutet. Ein Wert von -1 zeigt an, dass die Vektoren genau entgegengesetzt verlaufen, was vollständige Unähnlichkeit darstellt. In der praktischen NLP-Anwendung deuten Werte nahe 1 auf semantisch ähnliche Texte hin, während Werte nahe 0 auf nicht zusammenhängende Inhalte hindeuten.
Die Kosinus-Ähnlichkeit wird für Text-Embeddings bevorzugt, weil sie den Winkel zwischen Vektoren misst und nicht deren absolute Distanz, sodass sie unempfindlich gegenüber der Vektorlänge bleibt. Das ist für NLP entscheidend, da die Dokumentlänge die semantische Ähnlichkeit nicht beeinflussen sollte – eine kurze Anfrage und ein langer Artikel können gleichermaßen relevant sein. Die euklidische Distanz hingegen ist empfindlich gegenüber der Größe und funktioniert schlecht in hochdimensionalen Räumen, in denen Vektoren oft konvergieren. Die Kosinus-Ähnlichkeit ist außerdem recheneffizienter und liegt stets zwischen -1 und 1, wodurch Überlaufprobleme vermieden werden.
In RAG-Systemen ermöglicht die Kosinus-Ähnlichkeit die Retrieval-Phase, indem sie Abfrage-Embeddings mit Dokument-Embeddings in einer Vektordatenbank vergleicht. Wenn ein Nutzer eine Anfrage stellt, wird diese mit demselben Embedding-Modell wie die gespeicherten Dokumente in einen Vektor umgewandelt. Die Kosinus-Ähnlichkeit ordnet daraufhin die Dokumente nach Relevanz, wobei höhere Werte bessere Übereinstimmungen anzeigen. Die bestplatzierten Dokumente werden abgerufen und dem LLM als Kontext bereitgestellt, was genauere und faktenbasierte Antworten ermöglicht. Dieser Prozess hilft RAG-Systemen, LLM-Einschränkungen wie veraltetes Wissen und Halluzinationen zu überwinden.
Die Kosinus-Ähnlichkeit hat mehrere Einschränkungen: Sie ist nicht definiert, wenn Vektoren die Länge Null haben, weshalb eine Vorverarbeitung zur Entfernung von Nullvektoren erforderlich ist. Sie kann irreführend hohe Ähnlichkeitswerte für ausgerichtete, aber semantisch unzusammenhängende Vektoren liefern – insbesondere bei schlecht trainierten Embeddings. Das Maß ist zudem symmetrisch, kann also die Vergleichsrichtung nicht unterscheiden, was in bestimmten Anwendungen problematisch sein kann. Außerdem bedeutet ein Wert von 0 nicht immer vollständige Unähnlichkeit im realen Kontext, insbesondere in nuancierten Bereichen wie Sprache, wo orthogonale Vektoren dennoch semantische Beziehungen aufweisen können.
Die Kosinus-Ähnlichkeit wird mit folgender Formel berechnet: (A · B) / (||A|| × ||B||), wobei A · B das Skalarprodukt der Vektoren A und B ist, und ||A|| sowie ||B|| deren Beträge (euklidische Normen). Das Skalarprodukt berechnet sich, indem jeweilige Vektorkomponenten multipliziert und die Ergebnisse addiert werden. Die Länge eines Vektors ist die Quadratwurzel der Summe seiner quadrierten Komponenten. Diese Formel liefert einen normalisierten Wert zwischen -1 und 1 und ist dadurch unabhängig von der Vektorlänge, was Vergleiche unterschiedlich großer Vektoren ermöglicht.
In KI-Monitoring-Plattformen wie AmICited ist die Kosinus-Ähnlichkeit entscheidend, um Marken- und Domain-Erwähnungen in KI-Systemen wie ChatGPT, Perplexity und Google AI Overviews zu verfolgen. Durch die Umwandlung von Marken-Erwähnungen und Abfragen in Vektorembeddings misst die Kosinus-Ähnlichkeit, wie stark KI-generierte Antworten mit überwachten Inhalten übereinstimmen. So können Unternehmen überprüfen, ob ihre Domains in KI-Antworten erscheinen, die semantische Relevanz von Erwähnungen bewerten und nachvollziehen, wie KI-Systeme ihre Inhalte gegenüber Wettbewerbern referenzieren. Die Effizienz dieses Maßes ermöglicht Echtzeitüberwachung von Millionen KI-Interaktionen.
Wichtige KI-Plattformen und Tools, die die Kosinus-Ähnlichkeit nutzen, sind die Embedding-Modelle von OpenAI, Googles semantische Suchalgorithmen, das Antwortgenerierungssystem von Perplexity und die Retrieval-Mechanismen von Claude. Vektordatenbanken wie Pinecone, Weaviate und Milvus verwenden die Kosinus-Ähnlichkeit als primäres Ähnlichkeitsmaß. Open-Source-Bibliotheken wie Scikit-learn, TensorFlow, PyTorch und NumPy bieten eingebaute Funktionen für Kosinus-Ähnlichkeit. PostgreSQL mit der Erweiterung pgvector ermöglicht Kosinus-Ähnlichkeits-Berechnungen im großen Maßstab. Diese Tools treiben Empfehlungssysteme, Chatbots, semantische Suchmaschinen und RAG-Anwendungen im gesamten KI-Ökosystem an.
Beginnen Sie zu verfolgen, wie KI-Chatbots Ihre Marke auf ChatGPT, Perplexity und anderen Plattformen erwähnen. Erhalten Sie umsetzbare Erkenntnisse zur Verbesserung Ihrer KI-Präsenz.

Entdecken Sie, welche Faktoren am stärksten mit der KI-Sichtbarkeit korrelieren. Erfahren Sie, wie Marken-Nennungen, Suchvolumen und Ankertexte die KI Overviews...

Erfahren Sie, was ein KI-Sichtbarkeitsindex ist, wie er Zitierhäufigkeit, Position, Sentiment und Reichweite kombiniert und warum er für die Markensichtbarkeit ...
Ko-Vorkommen liegt vor, wenn verwandte Begriffe gemeinsam in Inhalten erscheinen und Suchmaschinen sowie KI-Systemen semantische Relevanz signalisieren. Erfahre...
Cookie-Zustimmung
Wir verwenden Cookies, um Ihr Surferlebnis zu verbessern und unseren Datenverkehr zu analysieren. See our privacy policy.