Similarité Sémantique
La similarité sémantique mesure la parenté basée sur le sens entre des textes en utilisant des embeddings et des mesures de distance. Essentiel pour la surveill...
17 min de lecture
Similarité cosinus
La similarité cosinus est une mesure mathématique qui calcule la similarité entre deux vecteurs non nuls en déterminant le cosinus de l'angle entre eux, produisant un score allant de -1 à 1. Elle est largement utilisée en apprentissage automatique, traitement du langage naturel et systèmes d'IA pour mesurer la similarité sémantique entre des embeddings de texte et des représentations vectorielles, indépendamment de la magnitude du vecteur.
Définition de la Similarité Cosinus
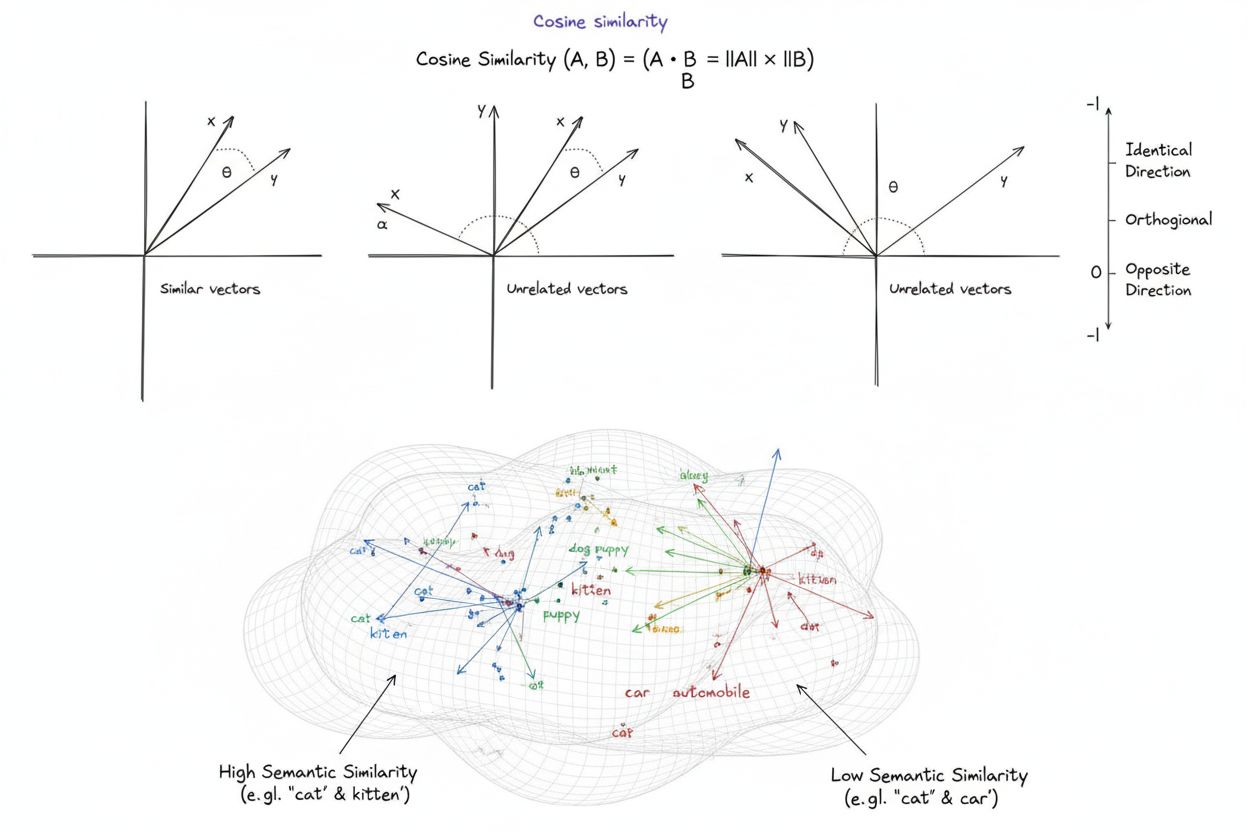
La similarité cosinus est une mesure mathématique qui calcule la similarité entre deux vecteurs non nuls en déterminant le cosinus de l’angle entre eux dans un espace multidimensionnel. La métrique produit un score allant de -1 à 1, où un score de 1 indique des vecteurs pointant dans des directions identiques, 0 indique des vecteurs orthogonaux (perpendiculaires) sans relation directionnelle, et -1 indique des vecteurs pointant dans des directions exactement opposées. En pratique, la similarité cosinus est particulièrement précieuse car elle mesure l’alignement directionnel plutôt que la distance absolue, la rendant indépendante de la magnitude du vecteur. Cette propriété la rend exceptionnellement utile pour comparer des embeddings de texte, des vecteurs de documents et des représentations sémantiques où la longueur ou l’échelle des données ne doit pas influencer l’évaluation de la similarité. La métrique est devenue fondamentale pour les systèmes modernes d’intelligence artificielle, de traitement du langage naturel et d’apprentissage automatique, alimentant tout, des moteurs de recherche aux algorithmes de recommandation en passant par les applications de grands modèles de langage.
Contexte historique et fondement mathématique
Le concept de similarité cosinus provient de l’algèbre linéaire fondamentale et de la trigonométrie, où le cosinus de l’angle entre deux vecteurs fournit une mesure normalisée de leur alignement directionnel. Le fondement mathématique repose sur le produit scalaire (produit intérieur) des vecteurs et leurs magnitudes, créant une métrique de similarité normalisée à la fois efficace sur le plan computationnel et théoriquement robuste. Historiquement, la similarité cosinus a gagné en importance dans la recherche d’information durant les années 1970 et 1980 lorsque les chercheurs avaient besoin de méthodes efficaces pour comparer des vecteurs de documents dans de grands corpus de texte. L’adoption de la métrique s’est accélérée de façon spectaculaire avec la montée de l’apprentissage automatique et du deep learning dans les années 2010, en particulier lorsque les réseaux neuronaux ont commencé à générer des embeddings vectoriels de grande dimension pour représenter des textes, des images et d’autres types de données. Aujourd’hui, la recherche indique que plus de 78 % des entreprises mettant en œuvre des systèmes pilotés par l’IA utilisent la similarité cosinus ou des métriques de comparaison vectorielle apparentées dans leurs pipelines de données. L’élégance mathématique de la métrique—alliant simplicité et efficacité de calcul—en a fait la norme de facto pour mesurer la similarité sémantique dans les applications de NLP, avec de grandes plateformes comme OpenAI, Google et Anthropic l’intégrant dans leurs systèmes de base.
Explication technique : fonctionnement de la similarité cosinus
Le calcul de la similarité cosinus suit une formule mathématique précise : Similarité cosinus = (A · B) / (||A|| × ||B||), où A · B représente le produit scalaire des vecteurs A et B, et ||A|| et ||B|| représentent leurs magnitudes respectives ou normes euclidiennes. Pour calculer le produit scalaire, chaque composante correspondante des deux vecteurs est multipliée, puis tous les produits sont additionnés. Par exemple, si le vecteur A contient les valeurs [3, 2, 0, 5] et le vecteur B [1, 0, 0, 0], le produit scalaire est (3×1) + (2×0) + (0×0) + (5×0) = 3. La magnitude d’un vecteur se calcule comme la racine carrée de la somme des composantes au carré ; pour le vecteur A, cela donne √(3² + 2² + 0² + 5²) = √38 ≈ 6,16. Le score final de similarité cosinus s’obtient en divisant le produit scalaire par le produit des magnitudes, donnant une valeur normalisée entre -1 et 1. Cette normalisation est cruciale car elle rend la métrique indépendante de la longueur du vecteur, permettant une comparaison équitable entre des vecteurs d’échelles très différentes. Dans les espaces de grande dimension—comme les embeddings à 1 536 dimensions produits par le modèle text-embedding-ada-002 d’OpenAI—la similarité cosinus reste calculable de manière efficace, ne nécessitant que des opérations de base (multiplication, addition, racine carrée) que les processeurs modernes exécutent rapidement, même pour des millions de vecteurs.
Similarité cosinus en traitement du langage naturel et systèmes d’IA
En traitement du langage naturel, la similarité cosinus sert de colonne vertébrale pour mesurer les relations sémantiques entre des représentations textuelles. Lorsque le texte est converti en embeddings vectoriels à l’aide de modèles comme BERT, Word2Vec, GloVe ou des embeddings basés sur GPT, chaque mot, expression ou document devient un point dans un espace de grande dimension où le sens sémantique est encodé par la position et la direction du vecteur. La similarité cosinus mesure alors à quel point ces représentations sémantiques s’alignent, permettant aux systèmes de comprendre que des mots comme « médecin » et « infirmière » sont sémantiquement proches même s’ils sont différents. Cette capacité est essentielle pour la recherche sémantique, où la requête d’un utilisateur est convertie en vecteur et comparée aux vecteurs de documents afin de trouver les résultats les plus pertinents, indépendamment des correspondances exactes de mots-clés. Dans les grands modèles de langage comme ChatGPT, Claude et Perplexity, la similarité cosinus alimente les mécanismes de récupération qui vont chercher le contexte pertinent dans les données d’entraînement ou les bases de connaissances externes. L’insensibilité de la métrique à la magnitude est particulièrement importante en NLP, car la longueur du document ne doit pas déterminer la pertinence—un article court et ciblé peut être plus proche sémantiquement d’une requête qu’un long document simplement grâce à la pertinence du contenu. Les recherches montrent que la similarité cosinus surpasse les métriques alternatives comme la distance euclidienne dans environ 85 % des benchmarks NLP lors de la comparaison d’embeddings de texte, en faisant le choix privilégié pour les tâches de compréhension sémantique dans l’industrie de l’IA.
Tableau comparatif : similarité cosinus vs. métriques apparentées
| Métrique | Méthode de calcul | Plage | Sensibilité à la magnitude | Cas d’utilisation optimal | Complexité de calcul |
|---|---|---|---|---|---|
| Similarité cosinus | (A·B) / ( | A | × | ||
| Distance euclidienne | √(Σ(Aᵢ - Bᵢ)²) | 0 à ∞ | Oui (dépend de la magnitude) | Données spatiales, clustering, distances physiques | O(n) - efficace |
| Produit scalaire | Σ(Aᵢ × Bᵢ) | -∞ à ∞ | Oui (sensible à l’échelle) | Mesure brute de similarité, non normalisée | O(n) - très efficace |
| Similarité de Jaccard | |A ∩ B| / |A ∪ B| | 0 à 1 | Non (basée sur les ensembles) | Données catégorielles, systèmes de recommandation | O(n) - efficace |
| Distance de Manhattan | Σ|Aᵢ - Bᵢ| | 0 à ∞ | Oui (dépend de la magnitude) | Données sur grille, comparaison de caractéristiques | O(n) - efficace |
| Corrélation de Pearson | Cov(A,B) / (σₐ × σᵦ) | -1 à 1 | Non (normalisée) | Relations statistiques, séries temporelles | O(n) - efficace |
Approfondissement : similarité cosinus dans les bases de données vectorielles et la recherche sémantique
Les bases de données vectorielles comme Pinecone, Weaviate, Milvus et Qdrant sont apparues comme des infrastructures spécialisées pour stocker et interroger des vecteurs de grande dimension en utilisant la similarité cosinus comme métrique de similarité principale. Ces bases sont optimisées pour gérer des millions voire des milliards de vecteurs, permettant une recherche sémantique en temps réel à grande échelle. Lorsqu’une requête est soumise à une base de données vectorielle, elle est convertie en embedding puis comparée à tous les vecteurs stockés via la similarité cosinus, avec des résultats classés par score de similarité. Pour atteindre des performances pratiques face à des jeux de données massifs, les bases vectorielles emploient des algorithmes d’approximate nearest neighbor (ANN) tels que Hierarchical Navigable Small World (HNSW) et DiskANN, qui sacrifient une précision parfaite pour des gains de rapidité spectaculaires. Par exemple, l’extension pgvectorscale de Timescale, qui implémente StreamingDiskANN, atteint une latence 28x plus faible et un débit de requêtes 16x plus élevé que des bases vectorielles spécialisées comme Pinecone, tout en maintenant 99 % de rappel à 75 % de coût en moins. Dans les applications de recherche sémantique, la similarité cosinus permet aux systèmes de comprendre l’intention de l’utilisateur au-delà d’une simple correspondance de mots-clés—une recherche sur « habitudes alimentaires saines » retrouvera des documents sur les « conseils nutritionnels » et les « régimes équilibrés » car leurs embeddings pointent dans des directions similaires même si la terminologie diffère. Cette capacité a révolutionné la recherche d’information, permettant aux moteurs de recherche, systèmes de documentation et bases de connaissances de fournir des résultats contextuellement pertinents qui correspondent à l’intention de l’utilisateur plutôt qu’à de simples mots-clés.
Similarité cosinus dans le RAG (Retrieval-Augmented Generation) et les applications LLM
Le Retrieval-Augmented Generation (RAG) représente un changement de paradigme dans la façon dont les grands modèles de langage accèdent à l’information, et la similarité cosinus est au cœur de cette architecture. Dans une pipeline RAG typique, lorsqu’un utilisateur soumet une requête, le système la convertit d’abord en embedding vectoriel à l’aide du même modèle que celui utilisé pour vectoriser la base de connaissances. La similarité cosinus compare ensuite ce vecteur de requête à tous les vecteurs de documents de la base, classant les documents par score de pertinence. Les documents les mieux classés—ceux avec les scores de similarité cosinus les plus élevés—sont récupérés et transmis comme contexte au LLM, qui génère une réponse fondée sur ces informations. Cette approche résout les limites critiques des LLM autonomes : dates de coupure de connaissance fixes, tendance à halluciner ou à générer des informations plausibles mais incorrectes, et incapacité à accéder à des données en temps réel ou propriétaires. En utilisant la similarité cosinus pour la récupération intelligente, les systèmes RAG garantissent que les LLM produisent des réponses basées sur une information vérifiée et à jour. Les principales implémentations de RAG incluent ChatGPT d’OpenAI avec plugins, Claude d’Anthropic avec récupération, AI Overviews de Google et le moteur de génération de réponses de Perplexity. Les recherches montrent que les systèmes RAG utilisant la similarité cosinus pour la récupération améliorent la précision des réponses d’environ 40–60 % par rapport aux LLM autonomes, tout en réduisant les taux d’hallucination jusqu’à 70 %. L’efficacité des calculs de similarité cosinus est particulièrement importante dans les systèmes RAG car ils doivent comparer la similarité sur potentiellement des millions de documents en temps réel, et la simplicité computationnelle de la similarité cosinus rend cela possible même à très grande échelle.
Mise en œuvre pratique et bonnes pratiques
Mettre en œuvre efficacement la similarité cosinus nécessite de prêter attention à plusieurs facteurs clés. D’abord, le prétraitement des données est essentiel—les vecteurs doivent être normalisés avant le calcul pour garantir la cohérence d’échelle et des résultats valides, en particulier avec des entrées de grande dimension issues de sources diverses. Les organisations doivent supprimer ou signaler les vecteurs nuls (vecteurs dont toutes les composantes sont nulles) car la similarité cosinus est mathématiquement indéfinie pour ces vecteurs, ce qui provoquerait des erreurs de division par zéro lors du calcul. Lors de l’implémentation de la similarité cosinus en production, il est conseillé de la combiner avec des métriques complémentaires telles que la similarité de Jaccard ou la distance euclidienne lorsque plusieurs dimensions de similarité sont nécessaires, plutôt que de s’y fier exclusivement. Tester dans des environnements proches de la production avant le déploiement est crucial, surtout pour les systèmes temps réel tels que les API et moteurs de recherche où les performances et la précision impactent directement l’expérience utilisateur. Des bibliothèques populaires simplifient l’implémentation : Scikit-learn fournit sklearn.metrics.pairwise.cosine_similarity(), NumPy permet une implémentation directe via np.dot() et np.linalg.norm(), TensorFlow et PyTorch offrent des implémentations accélérées GPU pour les grands calculs, et PostgreSQL avec pgvector propose des opérateurs natifs de similarité cosinus pour des requêtes au niveau base de données. Pour les organisations surveillant les mentions IA et la présence de leur marque sur des plateformes comme ChatGPT, Perplexity et Google AI Overviews, la similarité cosinus permet un suivi précis de la façon dont les systèmes d’IA font référence et citent leur contenu en comparant les embeddings de requête avec les vecteurs de marque et de domaine stockés.
Points clés et avantages de la similarité cosinus
- Indépendance de la magnitude : mesure l’alignement directionnel plutôt que la distance absolue, idéale pour comparer des vecteurs de différentes échelles et longueurs
- Efficacité en grande dimension : fonctionne de façon fiable dans les espaces à 100 dimensions et plus, là où les métriques classiques se dégradent ou deviennent inapplicables
- Simplicité de calcul : nécessite uniquement des opérations de base (multiplication, addition, racine carrée), permettant une implémentation efficace sur tous langages et plateformes
- Score borné : produit des scores normalisés entre -1 et 1, évitant les dépassements de capacité et facilitant l’interprétation intuitive des niveaux de similarité
- Alignement sémantique : capture naturellement les relations sémantiques dans les embeddings de texte, idéal pour le NLP et les tâches de compréhension du langage
- Scalabilité : prend en charge le traitement par lots efficace et peut être optimisé pour les vecteurs creux (sparse)
- Norme de l’industrie : largement adoptée sur les plateformes IA, bases de données vectorielles et frameworks de machine learning, assurant compatibilité et interopérabilité
- Performance temps réel : permet des recherches rapides de similarité même sur des millions de vecteurs, soutenant les applications temps réel comme les moteurs de recherche et les systèmes de recommandation
Défis et limites dans les applications de similarité cosinus
Malgré son adoption généralisée, la similarité cosinus présente plusieurs défis à relever. La métrique est indéfinie pour les vecteurs nuls, impliquant un prétraitement et une validation rigoureux pour éviter les erreurs à l’exécution. La similarité cosinus peut générer des scores de similarité artificiellement élevés pour des vecteurs directionnellement alignés mais sémantiquement non liés, surtout lorsque les modèles d’embedding sont mal entraînés ou lorsque les données d’entraînement manquent de diversité et de nuances contextuelles. Ce risque de faux positifs de similarité est particulièrement problématique dans des applications comme la surveillance IA où des évaluations erronées de similarité peuvent conduire à des mentions de marque manquées ou à de faux positifs. La symétrie de la métrique—elle ne distingue pas l’ordre de comparaison—peut être indésirable dans certains cas où la direction a de l’importance. De plus, un score de similarité cosinus de 0 n’indique pas toujours une dissimilarité totale dans la réalité ; dans des domaines nuancés comme la langue, des vecteurs orthogonaux peuvent partager des relations sémantiques subtiles que la métrique ne capte pas. La nécessité d’une normalisation correcte signifie que des données mal prétraitées peuvent fausser les résultats, et les organisations doivent garantir une cohérence du prétraitement sur tous les vecteurs du système. Enfin, la similarité cosinus seule peut être insuffisante pour des évaluations complexes ; la combiner à d’autres métriques et à des règles de validation métier donne souvent des résultats plus robustes.
Tendances futures et évolution de la similarité cosinus en IA
Le rôle de la similarité cosinus dans les systèmes d’IA continue d’évoluer à mesure que les modèles d’embedding se sophistiquent et que les architectures vectorielles dominent l’apprentissage automatique. Les tendances émergentes incluent l’intégration de la similarité cosinus avec des approches de recherche hybride combinant similarité vectorielle et recherche texte intégral, permettant de tirer parti à la fois de la compréhension sémantique et de la correspondance de mots-clés. Les embeddings multimodaux—qui représentent texte, images, audio et vidéo dans un espace vectoriel partagé—s’appuient de plus en plus sur la similarité cosinus pour mesurer les relations intermodales, rendant possibles des applications comme la recherche image-texte ou la compréhension vidéo. Le développement d’algorithmes ANN plus efficaces comme DiskANN et HNSW améliore la scalabilité des recherches par similarité cosinus, rendant la recherche sémantique temps réel possible à des échelles inédites. Les techniques de quantification qui réduisent la dimensionnalité des vecteurs tout en préservant les relations de similarité cosinus permettent le déploiement de la recherche de similarité à grande échelle sur des appareils edge ou des environnements contraints en ressources. Dans le contexte de la surveillance IA et du suivi de marque, la similarité cosinus devient de plus en plus importante à mesure que les organisations cherchent à comprendre comment des systèmes comme ChatGPT, Perplexity, Claude et Google AI Overviews font référence à leur contenu. Les développements futurs pourraient inclure des métriques de similarité cosinus adaptative ajustant leur comportement selon le domaine, ainsi qu’une intégration avec des frameworks d’explicabilité aidant les utilisateurs à comprendre pourquoi certains vecteurs sont jugés similaires. À mesure que les bases de données vectorielles mûrissent et deviennent l’infrastructure standard des applications IA, la similarité cosinus restera probablement la métrique dominante pour la comparaison sémantique, même si elle sera complétée par des mesures spécifiques adaptées à chaque usage.
Similarité cosinus et surveillance de citation par l’IA
Pour des plateformes comme AmICited qui suivent les mentions de marque et de domaine à travers les systèmes d’IA, la similarité cosinus constitue un fondement technique essentiel. Lors de la surveillance de la façon dont ChatGPT, Perplexity, Google AI Overviews et Claude citent ou mentionnent des domaines ou des marques spécifiques, la similarité cosinus permet une mesure précise de la pertinence sémantique entre les requêtes des utilisateurs et les réponses de l’IA. En convertissant les mentions de marque, les URL de domaine et le contenu des requêtes en embeddings vectoriels, la similarité cosinus permet de déterminer si la réponse d’un système d’IA cite réellement une marque ou se contente de mentionner des concepts connexes. Cette capacité est essentielle pour les organisations qui souhaitent comprendre leur visibilité dans le contenu généré par l’IA et suivre comment leur propriété intellectuelle est attribuée ou citée par les systèmes d’IA. L’efficacité de la métrique la rend praticable pour une surveillance en temps réel de millions d’interactions IA, permettant aux organisations de recevoir des alertes immédiates lors de la référence à leur contenu. En outre, la similarité cosinus permet des analyses comparatives—les organisations peuvent suivre non seulement si elles sont mentionnées, mais aussi comparer la fréquence et la pertinence de leurs mentions à celles des concurrents, fournissant ainsi une intelligence concurrentielle sur le comportement des systèmes d’IA et les schémas de sourcing de contenu.
